Notebook

初心に帰ってベイズ線形多項式回帰(1)::8/5

日記 ベイズ 機械学習
時刻 行動
10:00 起床
13:00 外出
17:00 読書など

ベイズ線形回帰

おとといの記事日記(8/2):初心に帰って回帰分析 - 日記帳では，線形回帰モデルのパラメータを最尤推定というアプローチで決めた．

しかしながら，このモデルでは過学習を抑えるために正則化項というパラメータを設ける必要があった．そこで，ベイズ的な手法を導入することで，過学習を抑えることができ，なおかつモデルのパラメータ数がデータ数より多くなっても問題ないようだ．

解説の前にガウス分布は以下の法則を満たすことを紹介する．

[A]

${\bf x}$の周辺分布と${\bf x}$が与えられた際の${\bf y}$の条件付き分布が

$$ p({\bf x})=\mathcal N({\bf x}|\mu, \Lambda^{-1}) $$ $$ p({\bf y}|{\bf x})=\mathcal N({\bf y}|A{\bf x}+b,L^{-1}) $$

として与えられるとき，${\bf y}$の周辺分布と${\bf y}$が与えられた際の${\bf x}$の条件付き分布は

$$ p({\bf y})=\mathcal N({\bf y}|A\mu +b,L^{-1}+A\Lambda^{-1}A^{-1}) $$ $$ p({\bf x}|{\bf y})=\mathcal N({\bf x}|\Sigma(A^{T}L({\bf y}-b)+\Lambda \mu),\Sigma) $$ となる．ただし，$\Sigma=(\Lambda+A^{T}LA)^{-1}$である．

回帰モデルの尤度関数は入力$X$,目標${\bf t}$，基底関数$\phi(\cdot)$,精度$\beta=\sqrt{\sigma}^{-1}$に対し， $$ p({\bf t}|X,{\bf w},\beta)=\prod_{n=1}^{N}\mathcal N(t_n|{\bf w}^{T}\phi({\bf x}),\beta^{-1}) $$ と与えられることから，共役事前分布*1は

$$ p({\bf w})=\mathcal N({\bf w}|m_0,S_0) $$

のように書くことができる．

上で紹介した式変形[A]を使えば，事後分布$p({\bf w}|{\bf t})$は $$ p({\bf w}|{\bf t})=\mathcal N({\bf w}|m_N,S_N) $$ $$ m_N=S_N(S_0^{-1}m_0+\beta\Phi^{T}{\bf t}),S_N^{-1}=S_0^{-1}+\beta\Phi^{T}\Phi $$ $$ \Phi= \left[ \begin{array}{cccc} \phi_0(x_{1})&\phi_{1}(x_{1})&\cdots & \phi_{M -1}(x_{1})\\ \phi_0(x_{2})&\phi_1(x_{2})&\cdots&\phi_{M -1}(x_{2})\\ \vdots&\vdots&\ddots&\vdots\\ \phi_0(x_{N})&\phi_1(x_{N})&\cdots&\phi_{M -1}(x_{N})\\ \end{array} \right] $$ となる．また，ガウス分布は最頻値と期待値が一致するので，事後分布を最大化させる重み${\bf w}_{MAP}$は単に${\bf w}_{MAP}=m_N$である．

ここで，事前分布を簡単のために $$ p({\bf w}|\alpha)=\mathcal N({\bf w}|0,\alpha^{-1}I) $$ として与える．このとき，$m_N,S_N$は $$ m_N=\beta S_N\Phi^{T}{\bf t},S_N^{-1}=\alpha I+\beta\Phi^{T}\Phi $$ となる．

ここで，事後分布の対数を取ると $$ \ln p({\bf w}|{\bf t})=-\frac{\beta}{2}\sum^{N}_{n=1}(t_n-{\bf w}^{T}\phi({\bf x})_n)^{2}-\frac{\alpha}{2}{\bf w}^{T}{\bf w}+\text{Const} $$ となり，この関数の${\bf w}$に関する最大化は二乗和誤差と正則化項の和の最小化に一致することに等価であることが分かる．

このとき，入力${\bf x}$に対する$t$の予測確率分布は $$ p(t|{\bf t},\alpha, \beta)=\int p(t|{\bf w},\beta)p({\bf w}|{\bf t},\alpha,\beta)\text{d}{\bf w} $$ を評価すればよく， 条件付き分布が $$ p(t|{\bf x},{\bf w},\beta)=\mathcal N(t|m_N\phi({\bf x}),\beta^{-1}) $$ で，事後分布が上のように与えられていることから式変形[A]から，予測分布は $$ p(t|{\bf t},\alpha, \beta)=\mathcal N\left(t\bigg|m_N\phi({\bf x}),\frac{1}{\beta}+\phi({\bf x})^{T}S_N\phi({\bf x})\right) $$ として与えられる．

データから最適な$\alpha,\beta$を決める方法は，後日に紹介，実装するとして，まずはこのベイズ線形回帰モデルをPythonで実装する．

実装

import numpy as np
import matplotlib.pyplot as plt

class BayesLinearPolynomialRegression(object):
    def __init__(self, M=3, alpha=1e-2, beta=1):
        self.M = M
        self.alpha = alpha
        self.beta = beta
        
    def polynomialize(self, x):
        phi = np.array([x**i for i in range(self.M + 1)]).T
        return phi
    
    def fit(self, X, t):
        phi = self.polynomialize(X)
        self.w_s = np.linalg.inv(self.alpha * np.eye(phi.shape[1])
                                 + self.beta * phi.T.dot(phi))
        self.w_m = self.beta * self.w_s.dot(phi.T.dot(t))
        
    def predict(self, x):
        phi = self.polynomialize(x)
        t_m = phi.dot(self.w_m)
        t_v = 1/self.beta + np.sum(phi.dot(self.w_s) * phi, axis=1)
        t_s = np.sqrt(t_v)
        return t_m, t_v

polynomializeメソッドはサンプル点集合${\bf x}={x_n}$に基底関数を施し，以下のように定義される$\Phi$を生成するメソッドである*2

今回は多項式基底関数を用いたため，最右辺のような行列を生成する． $$ \Phi= \left[ \begin{array}{cccc} \phi_0(x_{1})&\phi_{1}(x_{1})&\cdots & \phi_{M -1}(x_{1})\\ \phi_0(x_{2})&\phi_1(x_{2})&\cdots&\phi_{M -1}(x_{2})\\ \vdots&\vdots&\ddots&\vdots\\ \phi_0(x_{N})&\phi_1(x_{N})&\cdots&\phi_{M -1}(x_{N})\\ \end{array} \right]= \left[ \begin{array}{cccc} x_{1}^{0}&x_{1}^{1}&\cdots & x_{1}^{M -1}\\ x_{2}^{0}&x_{2}^{1}&\cdots & x_{2}^{M -1}\\ \vdots&\vdots&\ddots&\vdots\\ x_{N}^{0}&x_{N}^{1}&\cdots & x_{N}^{M -1}\\ \end{array} \right] $$

fit及びpredictは，上記の数式を愚直に実装すればよいのだが，predictにおいて複数の点を予測するため，$\phi$に対してではなく$\Phi$に対する予測をさせるため若干の式変形を行う．その際，内積が要素積の総和で表されることを利用する．

def sin(x):
    return np.sin(2*np.pi*x)

def generate_data(func, noise_scale, N):
    x = np.random.uniform(size=N)
    t = func(x) + np.random.normal(scale=noise_scale, size=x.shape)
    return x, t

def display_predict(truefunc, X_train, t_train, X_test, t_test_m, t_test_s,text=None,name=None):
    fig = plt.figure(figsize=(8,6))
    plt.fill_between(X_test, t_test_m-t_test_s, t_test_m+t_test_s,color='r',alpha=0.25)
    plt.plot(X_test, truefunc(X_test), label='Target Curve', c='blue')
    plt.scatter(X_train, t_train, facecolors='none', edgecolors='black', label='Observated Points', alpha=0.6)
    plt.plot(X_test, t_test_m, c='r', label='Predict Curve')
    if text is not None:
        plt.title(text)
    plt.xlabel('$x$')
    plt.ylabel('$t$')
    plt.legend()
    plt.ylim((-1.5,1.5))
    if name is not None:
        plt.savefig('{}.png'.format(name))
        plt.close()
    else:
        plt.show()

補助関数を定義する．上から，目的曲線関数，データ生成関数，グラフ表示関数である．display_predictの引数はそれぞれ実曲線，訓練データX軸，訓練データt軸，テストデータX軸，テストデータt軸の平均，標準偏差．．．である． この関数を実行すると下記のような，$\pm \sigma$の範囲が赤く塗られた図が生成される．

f:id:Fgjiutx:20180805213332p:plain

X_train, t_train = generate_data(sin, 0.15,60)

model = BayesLinearPolynomialRegression(M=20, alpha=1e-3, beta=5)

model.fit(X_train, t_train)

X_test = np.linspace(0,1,200)
t_m, t_s = model.predict(X_test)

display_predict(sin, X_train, t_train, X_test, t_m, t_s)

データ数，$\alpha,\beta$を変えた際の予測の変化の様子は以下のようになる．

たしかに，$\alpha$が正則化係数として，$\beta$が制度の範囲を制御するパラメータとして働いていることが分かる．

次はエビデンス近似をまとめたい

*1:尤度をかけて事後分布を求めると、その関数形が同じになるような事前分布のこと．参照:【ベイズ統計】共役事前分布とは？わかりやすく解説 | 全人類がわかる統計学

*2:日記(8/2):初心に帰って回帰分析 - 日記帳

初心に帰って回帰分析::8/2

日記 プログラミング 機械学習
時刻 行動
11:00 起床
14:00 帰省開始
15:00 日吉駅発
18:00 土浦駅着
22:00 PRML読書

帰省するだけで結構疲れて辛いものがある．

PRML

1.1. 例:多項式曲線フィッティング

ベイズ理論ばっかり載ってるイメージのPRMLだけど最初の数ページは普通の回帰分析の例が載ってる． なので，折角ならと復習がてら回帰分析をイチから実装してみる．

回帰分析とは

そもそも回帰分析とは与えられた入力ベクトル{\bf x}\in \mathbb R^{D}から，目標値tの値を予測する問題だ．すなわち， t=f(x) と入力と出力の関係を表した時の関数fはどのように書けるかを求める問題といえる．

とりわけ，

\displaystyle t=w_0+w_1x_1+...+w_Dx_D

のように{\bf w}に関して線形になっているような回帰モデルのことは線形回帰モデルと呼ばれている．

しかしながら，こういったモデルは入力に関しても線形であるため，表現能力に乏しいという欠点がある．

そこで，入力ベクトルに対して，非線形な関数\phi_j({\bf x})を施してやることで，このモデルを以下のように拡張する({\bf w}に関して線形なのでこれも線形回帰モデル！！！)．

\displaystyle t=w_0+\sum_{j=1}^{M-1}w_j\phi_j({\bf x})={\bf w}^{T}{\bf \phi}({\bf x})

ただし，\phi_0({\bf x})=1である．この項は，関数の切片にあたるバイアス項である．

sinを多項式でフィッティングさせよう

今回は以下のようなsinに沿った値に対しノイズを加えた値{\bf t}を上記の例で\phi_j({\bf x})=x^{j}とした場合，すなわちM-1次多項式

\displaystyle t=w_0+w_1x+w_2x^{2}+...+w_{M-1}x^{M-1}

で入力と目標値との関係をモデル化する．

f:id:Fgjiutx:20180803011655p:plain

ただし，Mは設計者が任意に定めるパラメータである．

次に，このモデルにより予想された多項式曲線と目標値とのずれを定量化させる．こうすることで最適曲線の導出はこの関数の最小化により達成されることとなる．

この定量的なずれは誤差関数と呼ばれ，単純でかつよく用いられているものの例として二乗和誤差がある．このモデルの二乗和誤差Eは次式にて定義される．

\displaystyle E({\bf w})=\frac{1}{2}\sum_{n=1}^{N}({\bf w}^{T}{\bf \phi}({x_n}) - t_n),{\bf \phi}({x}):=[x^{0},x^{1},...,x^{M-1}]^{T}

これは，例えば曲線が次のように予測されたときの

f:id:Fgjiutx:20180803013858p:plain

距離の総和に等しい(下図中の紫線の和)

f:id:Fgjiutx:20180803013906p:plain

なお，誤差に1/2が掛けられているのは単に後々計算しやすくするためである*1．

ここで，N個のデータをまとめて処理するため，以下のように行列としてデータを扱うことにする．

$$ \Phi= \left[ \begin{array}{cccc} \phi_0(x_{1})&\phi_{1}(x_{1})&\cdots & \phi_{M -1}(x_{1})\\ \phi_0(x_{2})&\phi_1(x_{2})&\cdots&\phi_{M -1}(x_{2})\\ \vdots&\vdots&\ddots&\vdots\\ \phi_0(x_{N})&\phi_1(x_{N})&\cdots&\phi_{M -1}(x_{N})\\ \end{array} \right]= \left[ \begin{array}{cccc} x_{1}^{0}&x_{1}^{1}&\cdots & x_{1}^{M -1}\\ x_{2}^{0}&x_{2}^{1}&\cdots & x_{2}^{M -1}\\ \vdots&\vdots&\ddots&\vdots\\ x_{N}^{0}&x_{N}^{1}&\cdots & x_{N}^{M -1}\\ \end{array} \right] , {\bf t}= \left[ \begin{array}{c} t_{1}\\ t_{2}\\ \vdots\\ t_{N}\\ \end{array} \right] $$

すると二乗和誤差は以下のように表すことができる．

$$ E({\bf w})=\frac{1}{2}||\Phi{\bf w}-{\bf t}||_{2}^{2} $$

これの微分値が0となる点が最小(凸性より)なので，ちょちょっと計算すると，

$$ {\bf w}^{*}=(\Phi^{T}\Phi)^{-1}\Phi^{T}{\bf t} $$

のときに最小値をとることがわかる．

以下，この単純なモデルを実装する．

単純な線形回帰の実装

import numpy as np
import matplotlib.pyplot as plt

def generate_data(noise_scale, N):
    X_train = np.linspace(0, 1, N)
    t_train = np.sin(2*np.pi* X_train) + np.random.normal(scale=noise_scale,size=(N,))
    return X_train, t_train

def display_data(funcs, X, t,y_lim=(-1.4, 1.4),name=None,title=None):
    fig = plt.figure(figsize=(7,5))
    x = np.linspace(X.min(), X.max(), 200)
    plt.ylim(y_lim)
    if title is not None:
        plt.title(title)
    for func in funcs:
        plt.plot(x, func(x))
    plt.scatter(X, t, facecolors='none', edgecolors='r')
    if name is not None:
        plt.savefig("{}.png".format(name))
    else:
        plt.show()
    plt.close()

補助関数は，データ生成関数と画像の表示関数である．display_dataのfuncsにはfunctionのlistを渡す．

X_train, t_train = generate_data(0.3, 10)
X_test, t_test = generate_data(0.3, 30)

class SimpleMSE():
    def __init__(self,X_train, t_train):
        
        self.X_in = X_train
        self.t = t_train
    
    def fit(self, M=4,ndiv = 500):
        self.M = M
        phi = np.empty((self.X_in.shape[0],self.M))
        for i, col in enumerate(phi.T):
            phi[:,i] = self.X_in**i
        theta = np.linalg.solve(phi.T.dot(phi), phi.T.dot(self.t))
        func = lambda x: sum([th * x**i for i, th in zip(range(self.M), theta)])
        return theta, func

numpyには$Ax=b$に対して$x=A^{-1}b$を一発で求めるnp.linalg.solve(A, b)という関数があるのでそれで 重みを求める．

$M $をいろいろ変えた場合結果は以下のようになる．

$M=2$

f:id:Fgjiutx:20180803024146p:plain

$M=3$

f:id:Fgjiutx:20180803024113p:plain

$M=4$

f:id:Fgjiutx:20180803024135p:plain

$M=10$

f:id:Fgjiutx:20180803024153p:plain

$M=4$でいい感じに近似できているのに対し，$M=10$では入力画像に対して適合しすぎている． このような場合汎化性能*2としては低い．このような状態を過適合だとか過学習だとかいう．

過学習の防止方法

ここで，$M=4$の場合と$M=10$の場合の重みの値を比較してみると以下のようになる．

  • $M=4~$:

array([ -0.39173338, 9.61865923, -24.48746587, 15.07254699])

  • $M=10$:

array([-2.13642415e-01, 1.18629138e+02, -2.32840696e+03, 2.03425265e+04, -9.68996625e+04, 2.71673994e+05, -4.59441029e+05, 4.59632301e+05, -2.49977441e+05, 5.68794097e+04])

$M=10$のときの重みの値が$M=4$と比べてかなり大きいことが分かる．そのため，微小摂動に対する変化量が多くなり，モデル自体のノイズや未知データに対するロバスト性，汎化性がともに悪くなるといえる． そこで，先ほどの二乗和誤差に対し，重みに応じて誤差を足す罰則項*3を課す．このようにして，モデルの過学習を防ぐ方法を正則化(regularization)という．

$$ E({\bf w})=\frac{1}{2}||\Phi{\bf w}-{\bf t}||_{2}^{2}+\frac{\lambda}{2}||{\bf w}||_2^{2} $$

ただし，$\lambda$は設計者が任意に設定するパラメータで二乗和誤差と正則化誤差の相対的な重要度を表す．

これの微分も簡単にでき，最適値は

$$ {\bf w}^{*}=(\Phi^{T}\Phi+\lambda I)^{-1}\Phi^{T}{\bf t} $$

となる．

改めてこれを考慮し実装しなおす．

class SimpleMSE():
    def __init__(self,X_train, t_train):
        
        self.X_in = X_train
        self.t = t_train
    
    def fit(self, M=4,l2_penalty=0 ,ndiv = 500):
        self.M = M
        phi = np.empty((self.X_in.shape[0],self.M))
        for i, col in enumerate(phi.T):
            phi[:,i] = self.X_in**i
        #### 変更箇所
        theta = np.linalg.solve(phi.T.dot(phi)+l2_penalty*np.eye(self.M), phi.T.dot(self.t))
        ####
        func = lambda x: sum([th * x**i for i, th in zip(range(self.M), theta)])
        return theta, func

このようにして$M=10,\lambda=10^{-4}$として実行すると以下のようになる．

f:id:Fgjiutx:20180803025456p:plain

うまく正則化が働いて元の曲線にかなり近似できていることが見て取れる．

$\lambda$を変えた際の曲線の変化の様子を動画にした．

youtu.be

うまく値を適合させるためには適切な値を与えてやる必要があることが分かる．

ここで値の適応具合を定量的に評価するため，平均二乗平方根誤差

$$E_{R M S}=\sqrt{\frac{2E({\bf w}^{*})}{N}}$$

を導入する．

$N$で割ることで，サイズの異なるデータを比較でき，平方根を取ることで目的変数と同じ単位での評価が可能となる．

def calc_mse_rmse(func, X_train, t_train):
    t_pred = np.array([func(x) for x in X_train])
    mse = 0.5*np.sum(np.square(t_pred - t_train))
    rmse = np.sqrt(2*mse/X_train.shape[0])
    return mse, rmse

mse = SimpleMSE(X_train, t_train)
rmse1 = []
rmse2 = []
i = 0
lms = np.logspace(-20, 1, 100)
for lm in lms:
    i += 1
    theta, func = mse.fit(10, lm)
    display_data([lambda x:np.sin(2*np.pi * x), func],
                 X_train, 
                 t_train,
                 name="./imgs/{:03d}".format(i),
                 title="$M = 9,\lambda = {:.3e}$".format(lm))
    _, rmse_train = calc_mse_rmse(func, X_train, t_train)
    _, rmse_test = calc_mse_rmse(func, X_test, t_test)
    rmse1.append(rmse_train)
    rmse2.append(rmse_test)

fig = plt.figure(figsize=(7,5))
plt.plot(lms, rmse1, label="Train_data")
plt.plot(lms, rmse2, label="Test_data")
plt.legend()
plt.xscale('log')
plt.xlabel('$\lambda$')
plt.ylabel('$E_{RMS}$')
plt.ylim((-0.05,1.05))
plt.show()

前半部分は動画を作るためのフレームの保存で，後半はRMS誤差のプロットである．

$\lambda$を$10^{-20}$から，$10^{1}$へ変化させていった際，RMS誤差は以下のような結果となった．

f:id:Fgjiutx:20180803030448p:plain

動画と比較して分かるように，元の曲線に近づくにしたがって，RMS誤差が減少していくのが分かる．

次はベイズ曲線フィッティングを実装したい．

*1:微分のためにです

*2:未知なるデータに対して妥当性の高い予測をするか

*3:penalty term．罰金項ともいう(PRMLでは罰金項であった)．

VAEって何？[実装編]::8/1

日記 機械学習 ベイズ 論文
時刻 行動
7:50 起床
10:00 バ始
19:00 バ終
21:00 帰宅
21:30 PRML読書
22:00 VAE実装の続き

Kerasを使ってVAEを実装する．

ライブラリをインポートする

import numpy as np
import matplotlib.pyplot as plt
import keras.backend as K
from IPython.display import clear_output
from keras.layers import *
from keras.models import Sequential, Model
from keras.optimizers import SGD, Adam, RMSprop
from utils.general.visualize import show_image
from keras.datasets import mnist

import plotly.plotly as py
import plotly.graph_objs as go
import plotly
from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl
import matplotlib.cm as cm

matplotlibのほかにplotly*1という可視化パッケージを使った．matplotlibと似たような使い方で，グリグリ動かせるグラフが作れる＋共有ができるようだ．

なおutils.general.visualizeは画像表示は頻繁に使う関数なので別ファイルで作成して，それを読み込んでいる．

utils/general/visualize.py
import matplotlib.gridspec as gs
import matplotlib.pyplot as plt
import os
import numpy as np

"""
visualize src images:
src: array-like object
"""
def show_image(src, col=4, row=4, size=(12,12),shuffle=False, path=None, name=None,channel_first=False,image_verbose=True):
    assert src.ndim==4 or src.ndim==3,"image dimension should be 3 or 4."
    if channel_first:
        src = np.rollaxis(src,1,4)
    assert src.ndim==3 or src.shape[-1] == (3 or 1),"number of channels should be 1 or 3"
    if src.shape[-1] ==1:
        src=src[:,:,:,0]
    n = col * row
    if shuffle:
        idx = np.random.permutation(src.shape[0])
        src=src[idx]
    plt.gray()
    src = src[:n]
    fig = plt.figure(figsize=size)
    g = gs.GridSpec(row,col)
    g.update(wspace=0.05, hspace=0.05)
    for i, sample in enumerate(src):
        ax = plt.subplot(g[i])
        plt.axis('off')
        ax.set_xticklabels([])
        ax.set_yticklabels([])
        ax.set_aspect('equal')
        plt.imshow(sample)
    if path is not None and name is not None:
        os.makedirs(path, exist_ok=True)
        if path[-1] == '/':
            path = path[:-1]
        plt.savefig("./{}/{}.png".format(path, name))
    if image_verbose:
        plt.show()
    else:
        plt.close()

データのロード

(x1, _), (x2, _) = mnist.load_data()
X = np.concatenate((x1,x2)).reshape((-1,28*28))/255.0
X.shape

testsetは生成モデルでは要らないので訓練画像(60000枚)とテスト画像(10000枚)を結合して[70000,784]のデータを作る．

モデルの作成

class VAE():
    def __init__(self, image_dim=784, hidden_dim=128, latent_dim=32, optimizer=None):
        self.im_dim = image_dim
        self.hd_dim = hidden_dim
        self.lt_dim = latent_dim
        if optimizer is None:
            self.optimizer = RMSprop()
        else:
            self.optimizer = optimizer
        self.model = self.model_compile(self.optimizer)
        
    def _build_encoder(self, input_dim=784, hidden_dim=128, latent_dim=32):
        in_layer = Input((input_dim,))
        hidden = Dense(hidden_dim,activation='relu')(in_layer)
        z_mean = Dense(latent_dim,activation='linear')(hidden)
        z_std = Dense(latent_dim,activation='linear')(hidden)
        return Model(in_layer, [z_mean, z_std])
    
    def _build_decoder(self, output_dim=784, hidden_dim=128, latent_dim=32):
        z_mean = Input((latent_dim,))
        z_std = Input((latent_dim,))
        sample = Lambda(self._sampling, output_shape=(self.lt_dim,))([z_mean, z_std])
        hidden = Dense(hidden_dim,activation='relu')(sample)
        decoded = Dense(output_dim,activation='relu')(hidden)
        return Model([z_mean, z_std], decoded)
    
    def _sampling(self, args):
        z_mean, z_std = args
        epsilon = K.random_normal((self.lt_dim,))
        return z_mean + z_std*epsilon
    
    def build_vae(self):
        self.encoder = self._build_encoder(self.im_dim, self.hd_dim, self.lt_dim)
        self.decoder = self._build_decoder(self.im_dim, self.hd_dim, self.lt_dim)

        in_layer = Input((self.im_dim,))
        z_mean, z_std = self.encoder(in_layer)
        ########
        self.z_m = z_mean
        self.z_s = z_std
        ########
        decoded = self.decoder([z_mean, z_std])
        vae = Model(in_layer, decoded)
        return vae

    def vae_loss(self, x_real, x_decoded):
        z_m2 = K.square(self.z_m)
        z_s2 = K.square(self.z_s)
        kl_loss = -0.5* K.mean(K.sum(1+K.log(z_s2)-z_m2-z_s2,axis=-1))
        rc_loss = K.mean(K.sum(K.binary_crossentropy(x_real, x_decoded),axis=-1),axis=-1)
        return kl_loss+rc_loss
    
    def model_compile(self, optimizer):
        vae = self.build_vae()
        vae.compile(optimizer=optimizer,loss=self.vae_loss)
        return vae

エンコーダ，デコーダともに隠れ層が1つだけの単純なMLPとした．

エンコーダの出力は潜在変数zの平均と標準偏差の2つがあるので，このような多入力多出力のようにちょっと複雑なモデルを作りたい際にはKeras Functional API*2が便利である． モデルの構造は大体こんな感じになってる． f:id:Fgjiutx:20180802011421p:plain

そして誤差は論文にある通り， f:id:Fgjiutx:20180802011944p:plain となるのでスッと実装する．

また，エンコーダの出力は誤差として使うのでメンバ変数に代入しとく(うえのコードの####で強調した部分)．

学習

vae = VAE(hidden_dim=64,latent_dim=3)

batch_size = 32
i = 0
batch_len = int(X.shape[0]//batch_size)
for epoch in range(10):
    np.random.shuffle(X)
    for batch in range(batch_len):
        X_minibatch = X[batch_size*(batch):batch_size*(batch+1)]
        if X_minibatch.shape[0] != batch_size:
            continue
        vae.model.train_on_batch(X_minibatch, X_minibatch)
        if batch%500==0:
            i += 1
            clear_output(True)
            print("epoch:{}, batch:{}/{}".format(epoch, batch, batch_len))
            image = vae.model.predict(X_minibatch)
            score = vae.model.evaluate(X_minibatch, X_minibatch)
            print("loss:{:.4f}".format(score))
            image = image.reshape((-1,28,28))
            show_image(image[:16])

今回は3次元の潜在変数へ投影する．

学習時間は高々5分弱だった．(GPU:NVidia GeForce GTX965m)

Matplotlibでの可視化

(_, _),(X_test, y_test) = mnist.load_data()

X_t = X_test[:800].reshape((-1,784))
y_t = y_test[:800]

z_t,_ = vae.encoder.predict(X_t)

800個のデータをエンコーダに通して次元圧縮する．

%matplotlib notebook
fig = plt.figure(figsize=(8,10))
ax = Axes3D(fig)
cmap = plt.get_cmap("jet",10)
norm = mpl.colors.Normalize(0, 9)
sm = cm.ScalarMappable(norm, cmap)
sm.set_array([])
divider = make_axes_locatable(ax)
fig.suptitle("VAE(ndim:784->3)")
ax.scatter3D(z_t[:,0],z_t[:,1],z_t[:,2],c=y_t,cmap=cm.jet)
plt.colorbar(sm, ticks=np.arange(0,10),boundaries=np.arange(-0.5,9.55,1),fraction=0.15,pad=0.1,orientation='horizontal')

jupyter上では%matplotlib notebookと書くことでグリグリ動かせるグラフが出力される．

(colormap周りの実装は結構忘れがちなので少し戸惑った．)

f:id:Fgjiutx:20180802013729p:plain

plotlyでの可視化

plot.ly

(↓グリグリできるヨ)

こんな感じにiframeで簡単に埋め込みができて便利． グリグリ動かして楽しもう．

cmap = [
    [0.0,'rgb(0, 0, 128)'],[0.1,'rgb(0, 0, 128)'],
    [0.1,'rgb(0, 0, 255)'],[0.2,'rgb(0, 0, 255)'],
    [0.2,'rgb(0, 99, 255)'],[0.3,'rgb(0, 99, 255)'],
    [0.3,'rgb(0, 213, 255)'],[0.4,'rgb(0, 213, 255)'],
    [0.4,'rgb(78, 255, 169)'],[0.5,'rgb(78, 255, 169)'],
    [0.5,'rgb(169, 255, 78)'],[0.6,'rgb(169, 255, 78)'],
    [0.6,'rgb(255, 230, 0)'],[0.7,'rgb(255, 230, 0)'],
    [0.7,'rgb(255, 125, 0)'],[0.8,'rgb(255, 125, 0)'],
    [0.8,'rgb(255, 20, 0)'],[0.9,'rgb(255, 20, 0)'],
    [0.9,'rgb(128, 0, 0)'],[1.0,'rgb(128, 0, 0)']
]

カラースケールの定義． plotlyでSpectralのカラーマップへの変更の仕方がいまいちわかんなかった．

trace = go.Scatter3d(
    x=z_t[:, 0],
    y=z_t[:, 1],
    z=z_t[:, 2],
    mode="markers",
    marker=dict(
        size=3,
        color=y_t,
        cmin=-0.5,
        cmax=9.5,
        colorscale=cmap,
        colorbar=dict(dtick=1)))
layout = go.Layout(margin=dict(l=0, r=0, b=0, t=0))
fig = go.Figure(data=[trace], layout=layout)
py.iplot(fig, filename="example")

案外楽な文法でつらつら書くだけでできる．

VAE関連の理解がまだ足りない気がするので積極的に論文を読んでいきたい．

PRML

夏休みを通じて確率統計の知見を深める会が計画されているらしいので，手元にあるPRMLを見始めた．

パターン認識と機械学習 上

パターン認識と機械学習 上

  • 作者: C.M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
  • 出版社/メーカー: 丸善出版
  • 発売日: 2012/04/05
  • メディア: 単行本（ソフトカバー）
  • 購入: 6人 クリック: 33回
  • この商品を含むブログ (20件) を見る

パターン認識と機械学習 下 (ベイズ理論による統計的予測)

パターン認識と機械学習 下 (ベイズ理論による統計的予測)

  • 作者: C.M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
  • 出版社/メーカー: 丸善出版
  • 発売日: 2012/02/29
  • メディア: 単行本
  • 購入: 6人 クリック: 14回
  • この商品を含むブログを見る

やはり結構難解で一筋縄ではいかない．頑張る．

*1:https://plot.ly/python/

*2:https://keras.io/ja/getting-started/functional-api-guide/

VAEって何？[殴り書き編]::7/31

日記 論文 機械学習 ベイズ
時刻 行動
7:40 起床
9:00 都市工学期末試験
12:00 メディア文化論期末レポート
13:30 夏休み！
14:00 論文読書
18:00 VRoid体験

めでたく夏休みに突入した．長期休暇何かとだらけがちになるので，意識して進捗を生んでいきたい所存(果たしてそのやる気がいつまで持つか…)

VAE

[1312.6114] Auto-Encoding Variational Bayes

hackmd.io

とりあえず原著論文を翻訳しただけのような状態なので理解がまだ3割くらい．

こんな感じで数日に一個くらい論文を読みたい気がある．

VRoid

すごい．髪の毛一瞬でふっさふさにできて気持ち良かった．

日記(7/23)

日記
時刻 行動
6:00 起床
9:45 大学着
10:30 グラフィック表現論期末試験
11:25 昼食
13:00 非線形工学期末試験
14:45 電気機器システム期末試験
17:00 帰宅
19:00 日課(Youtube)
22:00 日課(Twitter)

期末考査

想定以上に簡単だった気がする．特に非線形工学で履修した事柄はなんか他のことにも役立てそうではある．

実際にSpectral Norm GANでも行列のL_2ノルムを操作し，Lipschitz制約を満たすようにDiscriminatorの重みを変更している．

どうやらL_2ノルムは行列を作用素と見たときに自然に定義されるノルムらしく(詳しくはわからない)，重みを逐一||W||_2で割ってやることでDiscriminator全体が1-Lipschitzを満たすことができるようだ．

こう考えるとスペクトルノルムの導入はなかなか自然な感じがする．

実装

前に殴り書きした論文のまとめです．

hackmd.io

Kerasではいまいち動的にレイヤのパラメータ自体を操作させる方法が分からなかったので，どうにか調べていたらPytorchでの実装を発見した．

github.com

PytorchはChainer(この論文を書いたPFNが開発している！)同様，Define-by-Runが特徴のNNライブラリらしい．(というよりChainer経験者なら4時間くらいで凡そ理解できそうなくらい似てると思う)

今回は上のソースをほぼ写経したうえ,128\times128の 88860枚のアニメの顔画像をバッチサイズ32，潜在次元数256で学習を実行させた．

1エポックに大体5時間半掛かり，5エポック終わらせるのにおおよそ1日要した．

その結果，以下のようになった．なお潜在変数は固定した．その方がなんか学習してる感が出やすいと思ったので．

youtu.be

しかしこれだと既存のGANと比べてどうすごいのかいまいちわかんないなあ．

夏休みに入ったら学習結果の評価手法とかの論文も読み漁ってみたい所存

日記(7/20)

日記

精神的に余裕が出てきた．

ここ20日間やる気が極限まで低下していて何もする気が起きなかった．

Pythonでロジスティック写像(やったのは7/16)

非線形工学という講義を取っているんだが，内容が非常に高度でテスト前でもがき苦しんでる．でも，内容自体は非常に興味深いものが多く珍しく珍しくテスト対策にやる気が起きる教科でもある．

講義も終盤に差し掛かり，非線形の花形ともいえるカオス現象についての解説に入った．その中でも，導入に用いられたカオスの一つである，ロジスティック写像が非常に興味深かった． ロジスティック方程式は，もともと生物の個体の数を数理モデルに落とし込むために導入された方程式であり，連続な場合では以下の微分方程式で表される．

\displaystyle \frac{dx}{dt}=\alpha x(1-x)

上式においてxは個体数である．個体数は環境収容の限界であるx=1に近づくにつれて，その増加率は落ち込んでいく．また，\alphaは内的自然増加率と言われる定数である． 連続時間下ではこの式は非線形微分方程式であるが，変数分離法を用いて容易に解くことができ，

\displaystyle x=\frac{1}{1+(x_0^{-1}-1)e^{-\alpha t}}

のようになる． この解はS字を描き，

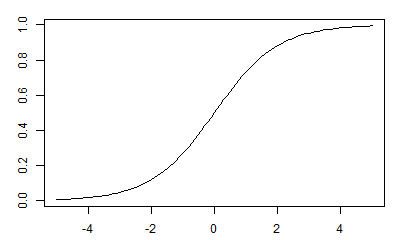
出典:第18回 ロジスティック回帰：機械学習 はじめよう｜gihyo.jp … 技術評論社

のようになる．この関数はロジスティック関数や，シグモイド関数などと呼ばれ， 機械学習分野でも，x_0=0.5とした，点(0,0.5)で点対称な関数を，ロジスティック回帰などのアルゴリズムで用いられる．

しかし，生物の増加を考えたとき離散時間で考えた方が世代の変遷が同時に行われると考えた下では妥当性が高い．そこで，先ほどの微分方程式を差分方程式へと変換する

{\displaystyle x\left[k+1 \right]=\alpha x\left[k \right](1- x\left[k \right])}

この方程式は連続時間内と大きく異なり，\alphaの値によって個体数の変動は非常に複雑となる． \alphaが小さなうちは連続時間と同様，一定の値に収束するが，\alpha\ge 3以上となると一定値に収束せず，2又，4又．．．と別れていき，\alpha=4に近づくにしたがって全くカオスな値を取るようになることが知られている． そこで離散時間におけるロジスティック写像の挙動をpythonでシミュレーションさせてみる．

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.lines as lines
import matplotlib.animation as anim
import os
from tqdm import tqdm

使うパッケージは上のヤツ．イツメンって感じ． 離散時間系の力学では，差分方程式を蜘蛛の巣図法と言われる手法で図的に表現することが可能である．

クモの巣図法 - Wikipedia

pythonで表すと以下のようになる

def calc_lines(func, init, num=300):
    vertices=[]
    nn = []
    yy = []
    
    x=init
    y=0
    vertices.append([x,y])
    nn.append(0)
    yy.append(x)
    
    for n in range(1, num):
        y = func(x)
        vertices.append([x, y])
        nn.append(n)
        yy.append(y)
        x=y
        vertices.append([x, y])
    return np.array(vertices), np.array(nn), np.array(yy)

x,yを入れ替えさえすればかなり容易に実装できる． あとはシミュレーションを行えばよい．

aaa = []
yyy = []
init = 0.3
os.makedirs("temp2",exist_ok=True)
for idx,a in enumerate(tqdm(np.arange(2.95,4.001,0.001))):
    fig = plt.figure(figsize=(12,8))
    fig.suptitle("$a=${:.4f}".format(a))
    ax3 = plt.subplot2grid((2,3), (0,1), rowspan=2,colspan=2)
    ax3.set_xlim(2.95, 4.0)
    ax3.set_ylim(0.0, 1.0)
    ax1 = plt.subplot2grid((2,3), (0,0))
    ax2 = plt.subplot2grid((2,3), (1,0))
    
    logistic = lambda x: a*x*(1-x)
    tt = np.arange(0.0, 1.0, 0.01)
    ax1.plot(tt, logistic(tt))
    ax1.plot(tt, tt)
    vs, ns, ys = calc_lines(logistic, init)
    ax1.plot(vs[:,0],vs[:,1],c='r',alpha=0.4,linestyle='-.')
    ax2.plot(ns, ys, alpha=0.7,marker='o')
    aa = np.ones((100,))*a
    aaa.append(aa)
    yyy.append(ys[-100:])
    ax3.scatter(aaa,yyy,c='black',s=1)
    plt.savefig("./temp2/{:04d}.png".format(idx))
    plt.close()
    del fig, ax1,ax2,ax3

変数名が死ぬほど適当だけどまあ気にしない．

メモリの都合上，300世代先までシミュレーションし，終わり100世代の個体数をプロットさせる． その結果として以下のようになる．

youtu.be

いい感じにカオスってて良い． 非線形は非常に興味の惹かれる分野であるが如何せん理論が難しく理解が困難なので頑張りをしていきたい気持ちがする．

ところで定期考査，死．

🐜(6/30)

🐜

動的計画法，解答見てあ〜ってなることしか出来なくて萎える．

動的計画法01

ナップサック問題

重量と価値が$w_i,v_i$である$N$個の荷物を，重量の総和が$W$を超えないように選んでナップサックに詰め込んだとき，価値の総和の最大値を出力せよ．

手法1

  1. メモ化再帰

  2. memsetによる初期化

手法2

  1. 漸化式からの直接DP(再帰不使用)

メモ化再帰を利用する

$\text{dp}[i][j]$を$i$番目以降の品物を重量が$j$以下になるようにナップサックに詰め込んだときの価値総和の最大値を表す$2$次元配列とすると， f:id:Fgjiutx:20180630214536p:plain 取り出さない状態と取り出して価値を比べた状態で 最大の方を選んでいけば良い．呼び出す際はrec(0,W)で再帰的に探索させてやれば良い．

メモ化再帰を用いないと再帰の深度が高くなり，計算量は $O(2^{n})$ となるが，メモ化を用いることで $O(NW)$まで減らすことができる．

int dp[1001][1001];

int rec(int i, int j)
{
    if (dp[i][j] >= 0)
        return dp[i][j];
    int res;
    if (i == N)
        return res = 0;
    else if (j < w[i])
        return res = rec(i + 1, j);
    else
        res = max(rec(i + 1, j), rec(i + 1, j - w[i]) + v[i]);
    return dp[i][j] = res;
}

int main()
{
    cin >> N >> W;
    memset(dp, -1, sizeof(dp));
    REP(i, N)
    {
        cin >> w[i];
    }
    REP(i, N)
    {
        cin >> v[i];
    }
    cout << rec(0, W) << endl;
    return 0;
}

漸化式を用いる

上記の漸化式の他，以下のように考えることが可能である．

今度は$\text{dp}[i+1][j]$を$i$番目までの品物から重量が$j$以下になるようにナップサックに詰め込んだときの価値総和の最大値を表す$2$次元配列とすると，

f:id:Fgjiutx:20180630214454p:plain

となる．漸化式を立てることができればforを用いて単純に以下のように実装することも可能．

計算量は見ての通り$O(NW)$で済む．

int dynamic()
{
    memset(dp, 0, sizeof(dp));
    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j <= W; j++)
        {
            if (w[i] > j)
            {
                dp[i + 1][j] = dp[i][j];
            }
            else
            {
                dp[i + 1][j] = max(dp[i][j],
                                   dp[i][j - w[i]] + v[i]);
            }
        }
    }
    return dp[N][W];
}

動的計画法02

重量と価値が$w_i,v_i$である$N$個の荷物を，重量の総和が$W$を超えないように選んでナップサックに詰め込んだとき，価値の総和の最大値を出力せよ．ただし，同一の荷物を複数詰め込んでも良い．

$\text{dp}[i+1][j]$を計算するに当たっては，荷物$i$を$k$個選んだうちの価値最大を格納すれば良いので，ナイーブに実装するなれば， $$ \text{dp}[i+1][j]\leftarrow\max(\text{dp}[i][j],{\text{dp}[i][j-kW[i]]+kV[i]|1\leq k}) $$ となるが，これでは計算量が$O(nW^{2})$となる．

ここでdpテーブルに着目してみると，$\text{dp}[i+1][j-W[i]]$にて，すでに荷物$~i~$を$k-~1$ 個選んだときの荷物の最大値が出ている．よって以下のようにすることで計算量を減らせる．

$$ \text{dp}[i+1][j]\leftarrow\max(\text{dp}[i][j],\text{dp}[i+1][j-W[i]]+V[i]) $$

(もちろん$j<W[i]$の場合分けを忘れずに！！)

int dp[1001][1001];
int N, W[1000], V[1000], w;

int dynamic()
{
    REP(i, N)
    {
        REP(j, w + 1)
        {
            if (j < W[i])
            {
                dp[i + 1][j] = dp[i][j];
                continue;
            }
            dp[i + 1][j] = max(dp[i][j], dp[i + 1][j - W[i]] + V[i]);
        }
    }
    return dp[N][w];
}

🐜本の進捗(6/25)

🐜 日記

本棚の奥底にあった蟻本を取り出した．

プログラミングコンテストチャレンジブック [第2版]　?問題解決のアルゴリズム活用力とコーディングテクニックを鍛える?

プログラミングコンテストチャレンジブック [第2版]　?問題解決のアルゴリズム活用力とコーディングテクニックを鍛える?

テンプレート

#include <bits/stdc++.h>
#define REP(i, n) for (int i = 0; i < n; i++)
#define REP2(i, st, ed) for (int i = st; i <= ed; i++)
using namespace std;

static const int inf = 1 << 28;

int main()
{
    return 0;
}

chaper 2

2-1 全探索問題

深さ優先探索01

部分和問題

数列${a_n}$から，要素をいくつか取り出して部分数列$b$を作る．入力$S$に対して，$b$の和が$S$となるような組み合わせは存在するか

アルゴリズム例

$i\leftarrow 0,s \leftarrow 0$

$dfs(index, sum):$

  1. $i=n$ならば終了
  2. 部分和に要素$a[i]$を．．．
    1. 含める$dfs(i+1,s+a[i])$
    2. 含めない$dfs(i+1,s)$
bool dfs(int i, int sum)
{
    if (i == n)
        return sum == k;
    if (dfs(i + 1, sum))
        return true;
    if (dfs(i + 1, sum + a[i]))
        return true;
}

深さ優先n探索02

8近傍島数算出問題

大きさ$n\times m~$の庭があります．そこに雨が降り，水たまりが出来ました．ある水たまりに対し，8近傍に隣接した水たまりがある場合その水たまりは連結していると考えます．いくつの水たまりがあるかを出力せよ．

void dfs(int x, int y)
{
    if (map[x][y] == 0 ||
        x < 0 || y < 0 ||
        x > n || y > m)
        return;
    map[x][y] = 0;
    REP2(i, -1, 1)
    {
        REP2(j, -1, 1)
        {
            dfs(x - i, y - j);
        }
    }
}

幅優先探索01

迷路探索

$n\times m~$の迷路に対し，最短経路でスタートからゴールに到達したときのステップ数を出力せよ．入力は.を通路，#を壁，Sを開始地点，Gをゴール地点とする．

  1. 距離をd=infでリセット

    $d(all)=\infty$

  2. 始点をd=0にして，キューに積む

    $d(start)=0$

    $Q.push(start)$

  3. キューのつづく限り以下の処理をする

    1. キューの先頭を取り出す

      $current = Q.pop()$

    2. ゴールならば抜ける

    3. 次の未探索かつ壁でない経路候補全てに以下の処理をする

      1. キューに積む

      2. d を更新する

      $d(next) \leftarrow d(current) + 1$

typedef pair<int, int> V;

int dx[4] = {-1, 0, 0, 1};
int dy[4] = {0, -1, 1, 0};

int bfs()
{
    queue<V> que;
    REP(i, n)
    {
        REP(j, m)
        {
            d[i][j] = INF;
        }
    }
    que.push(V(stx, sty));
    d[stx][sty] = 0;

    while (!que.empty())
    {
        V cur = que.front();
        que.pop();
        if (cur.first == gox && cur.second == goy)
            break;
        REP(i, 4)
        {
            int nx = cur.first + dx[i];
            int ny = cur.second + dy[i];

            if (0 <= nx && nx < n && 
                0 <= ny && ny < m &&
                mp[nx][ny] != '#' && d[nx][ny] == INF)
            {
                que.push(V(nx, ny));
                d[nx][ny] =
                     d[cur.first][cur.second] + 1;
            }
        }
    }
    return d[gox][goy];
}

2-2 貪欲法

貪欲法01

区間スケジューリング問題．

現在時間から選べるスケジュールのうち，最も早い時間に終わる ものを選択すると良い．

void greedy()
{
    sort(_pair, _pair + n);

    int ans = 0, t = 0;
    REP(i, n)
    {
        if (t < _pair[i].second)
        {
            ans++;
            t = _pair[i].first;
        }
    }
    cout << ans << endl;
}

貪欲法02

実践例：

$n$個の点が数直線状にあり，その座標は$X_i,(i=1,2,...,n)$である．その点のうちいくつかを選び印をつけるとする．印をつけた点から$r$の範囲内にすべての点$X_i$を含めるためには，最低いくつの点に印をつける必要があるか

直感的な発想を実装すればOK

void greedy()
{
    sort(p, p + n);
    int i = 0, ans = 0;
    while (i < n)
    {
        int s = p[i++];
        while (i < n && p[i] <= s + r)
            i++;
        int m = p[i - 1];
        while (i < n && p[i] <= m + r)
            i++;
        ans++;
    }
    cout << ans << endl;
}

貪欲法03

辞書順最小

$n$文字からなる文字列$S$の先頭または末端から取り出して，末端に連結してできる$n$文字の文字列$T$を考える．$T$のうち辞書順で最小となるものを出力せよ．

基本，先頭と末端の辞書順を比べる． 先頭と末端が同じ文字だった場合に，次に続く(先頭+1と末端-1)文字同士を比較して，辞書順で小さかった方の端の文字を出力すれば良い．for文で実装できるが終了条件に注意する．

void greedy()
{
    int a = 0, b = n - 1;
    bool left;
    while (a <= b)
    {
        for (int i = 0; a + i <= b; i++)
        {
            if (S[a + i] > S[b - i])
            {
                left = false;
                break;
            }
            else if (S[a + i] < S[b - i])
            {
                left = true;
                break;
            }
        }
        if (left)
            cout << S[a++];
        else
            cout << S[b--];
    }
    cout << endl;
}

貪欲法04

木こりは木を切りたい．切りたい長さは$L_1,L_2,...,L_n$であり，もとの長さはちょうどこの長さの和に等しい．板を切るためには板の長さ分のコストが掛かるとする．たとえば長さ$21$の板を$13$と$8$に分割した際にかかるコストは$21$である．コストが最小で木を切り分けたときのかかるコストはいくらか

  1. $sum\leftarrow 0$
  2. $\text{while}~~L.length()\geq2$
    1. $\text{sort}(L, \leq)$
    2. $m_1 = L.front(),m_2=L.front()$
    3. $L.popFront()\times 2$
    4. $sum\leftarrow sum+m_1+m_2$
    5. $L.pushFront(m_1+m_2)$
  3. $\text{return}~~sum$
vector<int> L;

void greedy()
{
    int ans = 0;
    while (L.size() >= 2)
    {
        sort(L.rbegin(), L.rend());
        int m1 = L.back();
        L.pop_back();
        int m2 = L.back();
        L.pop_back();
        ans += m1 + m2;
        L.push_back(m1 + m2);
    }
    cout << ans << endl;
}

#4 Improved Techniques for Training GANs

論文

 

https://arxiv.org/abs/1606.03498

要旨

半教師あり学習とリアリスティックな画像生成などのGANの応用に焦点を当ててアーキテクチャや訓練手順を提案する．

導入

GANは非凸ゲームのナッシュ均衡を多数のパラメータにより訓練し，求めることが必要． しかしながら，GANの学習には勾配降下が用いられ，ナッシュ均衡は使われていない．

GANの収束のための手法

Feature Matching

既存の直接，生成画像のディスクリミネータの評価関数を最大化させる手法のみではなく，ディスクリミネータの中間層の特徴量の期待値に一致させるようにジェネレータを訓練させる． 具体的には，${\bf f}({\bf \it{x}})$をディスクリミネータ中間層の活性化関数と定め，ジェネレータは次式で表される新しい評価関数を最小化させるように訓練する． $$||\mathbb{E}_{{\bf{\it x}}\sim p_{data}} {\bf f}({\bf{\it x}})- \mathbb{E}_{{\bf{\it z}}\sim {\it p}_{{\bf{\it z}}}} {\bf f}\left( {\it G}\left({\bf\it{z}}\right) \right)||_2^2 $$ 経験的に，GANが不安定になる状況下において，この手法が有効であることが示されている．

Minibatch Discrimination

モード崩壊の起こる状況下では，ディスクリミネータの勾配は多くの同様の点において，同一の方向を 指すことがある．ディスクリミネータは各々のサンプルを独立して処理するため， その勾配間の調整がなく，ジェネレータの出力がたがいにより似ないように指示する機構が存在しない． 勾配降下ではディスクリミネータが同一の画像をジェネレータから生成されることを学習するが学習過程において分離して考察することができない．

ミニバッチのサンプル間の近さをディスクリミネータに判別させることでこの問題を解決することができる．

そこで次のようなモデルを考える．${\bf f}(x_i) \in \mathbb R^A$をいま，ディスクリミネータの中間層にて生成される入力xix_iの特徴量のベクトルとする．このベクトルをテンソル$T\in \mathbb R^{A\times B\times C}$で掛け，行列$M_i\in\mathbb R^{B\times C}$を得たとする． この方法では，MiM_iのL1距離をサンプルごとに取り，負号の指数乗を取る．すなわちサンプルxi,xjx_i,x_jに対して，距離関数を $$ c_b(x_i,x_j)=\exp\left(-||M_{i,b}-M_{j,b}||_1 \right)\in\mathbb R $$ と定める．次にサンプルxix_iのこのミニバッチ層の出力o(xi)o(x_i)を以下のように定義する $$ \begin{eqnarray*} \displaystyle o(x_i)_b&=&\sum_{j=1}^nc_b(x_i,x_j)\in \mathbb R\\ \displaystyle o(x_i)&=&\left[ o(x_i)_1,o(x_i)_2, ... , o(x_i)_B\right]\in \mathbb R^B\\ \displaystyle o(X)&\in& \mathbb R^{n\times B} \end{eqnarray*} $$

このミニバッチ層の出力o(xi)o(x_i)と，入力である中間層特徴量f(xi)f(x_i)を連結させ，ディスクリミネータの次の層の入力に渡す．この層を適用することで，今までのようにディスクリミネータは各サンプルに対して，単一の数値を出力し訓練データか否かを示す機能を保ちつつ，側面的情報として， ニバッチ内の他のサンプルに関する情報を，ディスクリミネータに与えることが可能になる．

履歴平均

半教師あり学習

GANにおいて，ラベル数KKのラベルデータを用いて半教師あり学習を行う際は，ジェネレータから出力された画像を新たに，K+1K+1個めのクラスへと分類させるようにクラス分類器(=ディスクリミネータ)を 学習させてやればよいということが分かる．すなわち通常のGANにおける生成画像を看過するように学習する項1−D(x)1-D(x)と，このモデルにおけるpmodel(y=K+1|x)p_{model}(y=K+1|x)は等価であるといえる．

logpmodel(y∈{1,...,K}|x)\log p_{model}(y\in \{1,...,K\}|x)を最大化させることで，ラベルの降られていないデータに対しても，それに対応する実データのKKクラスに分類されるの1つの画像でクラス分類を行うことが可能になる．

実データと生成データを半々に含むようなデータセットに対して，損失関数は次のように定義できる．

$$ \begin{eqnarray*} L&=&-\mathbb E_{x,y\sim p_{data}(x,y)}[\log p_{model}(y|x)] -\mathbb E_{x\sim G}[\log p_{model}(y=K+1|x)]\\ &=&L_{supervised}+L_{unsupervised} \text{where}\\ L_{supervised}&=&-\mathbb E_{x,y\sim p_{data}(x,y)}[\log p_{model}(y|x,y<K+1)]\\ L_{unsupervised}&=&-\{\mathbb E_{x\sim p_{data}(x)}[\log p_{model}(y=K+1|x)] +\mathbb E_{x\sim G}[\log p_{model}(y=K+1|x)]\}\\ \end{eqnarray*} $$ このように分解することでこの損失関数は教師有り項に対しては，標準的なクロスエントロピー最適化問題と解釈でき，教師無し項は，D(x)=1−pmodel(y=K+1|x)D(x)=1-p_{model}(y=K+1|x)と定めることで， $$ L_{unsupervised}=-\{\mathbb E_{x\sim p_{data}(x)}\log D(x)+ \mathbb E_{z\sim noise}\log(1-D(G(z)))\} $$ となり，標準的なGANのディスクリミネータの損失関数に等しくなる．

実装上の観点では，K+1K+1もの出力を設ける必要がないことが言える．ソフトマックス層の出力は，各々の出力ljl_jに対してlj−f(x)l_j-f(x)のように任意関数の差分をとっても出力値に変化がないという特性を考慮すると，ディスクリミネータを D(x)=Z(x)Z(x)+1,whereZ(x)=∑k=1Kexp[lk(x)] D(x)=\frac{Z(x)}{Z(x)+1},\text{where}~~Z(x)=\sum_{k=1}^{K}\exp[l_k(x)] と定めることで，仮想的にpmodel(y|x,y<K+1)p_{model}(y|x,y<K+1)と等価になる．

ワンショット学習を行う際には，どのデータに対して，正解ラベルを与えるかが非常に重要である．