🐜本の進捗(優先度付きキューとUnionFind木)::9/13
いままでまともにアルゴリズムの勉強をしてこなかったので得るものが大きいです.
2-4 データ構造
二分木
すべてのノードの子の数が2以下の木
プライオリティキュー
数の追加と最小値の取り出しが行えるデータ構造を指す
二分木ヒープ
プライオリティキューを二分木を用いて実装したもの
子の数字>親の数字を満たす二分木で更新と削除のたびに左記条件を満たすまで交換を繰り返す.
実装方法
#include <bits/stdc++.h> using namespace std; #define REP(i, n) for (int i = 0; i < n; i++) template <typename T> class Heap { public: int sz = 0; T array[100001]; Heap() { } void push(T x) { int i = sz++; while (i > 0) { int p = (i - 1) / 2; if (array[p] <= x) break; array[i] = array[p]; i = p; } array[i] = x; } T pop() { T ret = array[0]; T x = array[--sz]; int i = 0; while (i * 2 + 1 < sz) { int a = i * 2 + 1, b = i * 2 + 2; if (b < sz && array[b] < array[a]) a = b; if (array[a] >= x) break; array[i] = array[a]; i = a; } array[i] = x; return ret; } }; int main(void) { Heap<float> heap; heap.push(1.6); heap.push(7.9); heap.push(-44.1); heap.push(842.0); heap.push(0.0); REP(i, 5) { cout << heap.pop() << endl; /* -44.1 0 1.6 7.9 842 */ } return 0; }
二分木なので親ノードのインデックスは(i-2)/2で取得でき,子ノードはi*2+1, i*2+2で取得が可能であることに注意しよう!!!!
$\text{function}~~push(Num: x) \rightarrow Nil$
- $arr = Array.new();sz = 0;//initialize$
- $i = sz++; // i \leftarrow \text{Self Node Index}$
- $\text{while}(i > 0):$
- $p = (i-1)/2; // p \leftarrow \text{Parent Node Index}$
- $\text{if}(arr[p] \leq x) \text{~then~~break;}$//逆転していたら抜ける
- $arr[i]=arr[p];~i=p;$
- $arr[i]=x$
$\text{function}~pop() \rightarrow Num$
- $retval = arr[0];$//返り値(最小値)
- $x = arr[-1];$//根に持ってくる値
- $i=0;$
- $\text{while}(i*2+1<sz):$//子ノードが存在する
- $l=i\times2+1,r=i\times2+2;$
- $\text{if}(r<sz$ $and$ $arr[b]<arr[a])\text{then}$ $a\leftarrow b;$
- $\text{if}(arr[a] \geq x)\text{thenbreak;}$
- $arr[i]=arr[a];~i=a;$
- $arr[i]=x;$
- $\text{return}~~retval;$
c++ のSTLにもプライオリティキューはある.そのため,イチから自分で実装するという機会はほぼないが,STLの方は最大値から取り出されるので注意が必要.
DS-1(POJ 2431)
壊れた燃料タンクを直すために距離が $L$ だけ離れている街へ向かう. タンクには最初 $P$ だけ燃料があるが,単位距離進む毎に1単位分の燃料を失う. 街までの道には $N$ 個の燃料補給所がある. $i$ 番目の補給所は故障地点から $A_i$ の位置にあり,そこで $B_i$ の燃料を補給することができる. タンクに保存できる燃料の量に上限は無い. 街まで進むために必要な最小の燃料補給の回数を答えよ. ただし,どのように進んでも街まで辿り着けない場合は $-1$ と出力せよ.
(POJ本家は街からの距離を$A_i$としていたが,蟻本では簡単のため故障地点からの位置に変えてある.)
ガソリンスタンドに寄って補給するのではなく,ガソリンスタンドに寄ったらそのガソリンスタンドで燃料を補給する権利を手に入れると考える.
つまり,通過したガソリンスタンドの補給量をPQに記憶し,燃料が尽きた地点で,立ち寄ったガソリンスタンドの中で最も補給量が大きいものを選べば良いことがわかる.
#include <queue> #include <iostream> using namespace std; #define REP(i, n) for (int i = 0; i < n; i++) int main() { int N, L, P; int A[10001], B[10001]; cin >> N; REP(i, N) { cin >> A[i]] >> B[i]; } cin >> L >> P; A[N] = L; B[N] = 0; N++; priority_queue<int> pq; int ans = 0, pos = 0, tank = P; REP(i, N) { int d = A[i] - pos; while (tank - d < 0) { if (pq.empty()) { cout << "-1" << endl; return 0; } tank += pq.top(); pq.pop(); ans++; } tank -= d; pos = A[i]; pq.push(B[i]); } cout << ans << endl; return 0; }
Union-Find木
グループ分けを管理するデータ構造の一種.次のことが効率的に行える.
- 要素$a$と要素$b$が同じグループに属するかを調べる
- 要素$a$と要素$b$のグループを併合する.分割は出来ない
一つの木を一つのグループとして扱う.
併合
木同士の根に辺を張ることで,グループを併合することができる.
要素判定
根が同じ要素同士は同一グループとみなすことができる.
実装上の注意
木構造を扱うので,深さに偏りが発生すると計算量が増大してしまう.そこで,各木の深さを記憶してとき,深さの浅い木を深い方に辺を張ることで偏りの少ない木とすることができる.
また,各ノードが根を辿った場合,辺を直接根に張り直すことで根からの深さを抑えることができる.
実装例
http://www.prefield.com/algorithm/container/union_find.html
class UnionFind{ private: vector<int> arr; public: UnionFind(int size): arr(size, -1){} int root(int node){ return arr[node] < 0 ? node : arr[node] = root(arr[node]); } int size(int x){ return -arr[root(x)]; } bool unionSet(int x, int y){ x = root(x); y = root(y); if(x!=y){ if(arr[x] < arr[y]) swap(x, y); arr[x] += arr[y]; arr[y] = x; } return x != y; } bool findSet(int x, int y){ return root(x) == root(y); } };
DS-2(POJ 1182)
$N$匹の動物に対し$1..N$の番号が振られており,各々の動物は3つの$A,B,C$に 分けられる.このグルーピングには以下のような強弱関係がある.$A\rightarrow B \rightarrow C \rightarrow A$.
次の2種類の情報が$k$個与えられる.
- $x$と$y$は同じ種類である
- $x$は$y$を捕食する
入力を逐次処理した際,矛盾する記述は何個あるか.ただし矛盾した記述は以降捨てると考える.
int main(void) { bool debug = true; int N, k; int T[50001], X[50001], Y[50001]; cin >> N >> k; REP(i, k) { scanf("%d %d %d", &T[i], &X[i], &Y[i]); } UnionFind uf = UnionFind(3 * N); int ans = 0; REP(i, k){ int t = T[i]; int x = X[i] - 1; int y = Y[i] - 1; if (x < 0 || x >= N || y < 0 || y>=N){ ans++; if (debug) cout << "[*] Invalid Data (Out of length): x = " << x << ", y = " << y << endl; continue; } // Same Group if(t==1){ if(uf.findSet(x, y+N) || uf.findSet(x, y+2*N)){ ans++; if (debug){ cout << "[*] Invalid 'Same kind' input: x = "; cout << x << ", y = " << y << endl; } }else{ uf.unionSet(x, y); uf.unionSet(x + N, y + N); uf.unionSet(x + 2 * N, y + 2 * N); if (debug){ cout << "[*] Valid 'Same kind' input: x = "; cout << x << ", y = " << y << endl; } } }else if(t == 2){ // Eat Group if(uf.findSet(x, y+N) || uf.findSet(x, y+2*N)){ ans++; if (debug){ cout << "[*] Invalid 'Eat kind' input: x = "; cout << x << ", y = " << y << endl; } }else{ uf.unionSet(x, y + N); uf.unionSet(x + N, y + 2*N); uf.unionSet(x + 2 * N, y); if (debug){ cout << "[*] Valid 'Eat kind' input: x = "; cout << x << ", y = " << y << endl; } } }else{ ans++; cout << "[*] Invalid Type: t = " << t; } } cout << ans << endl; return 0; }
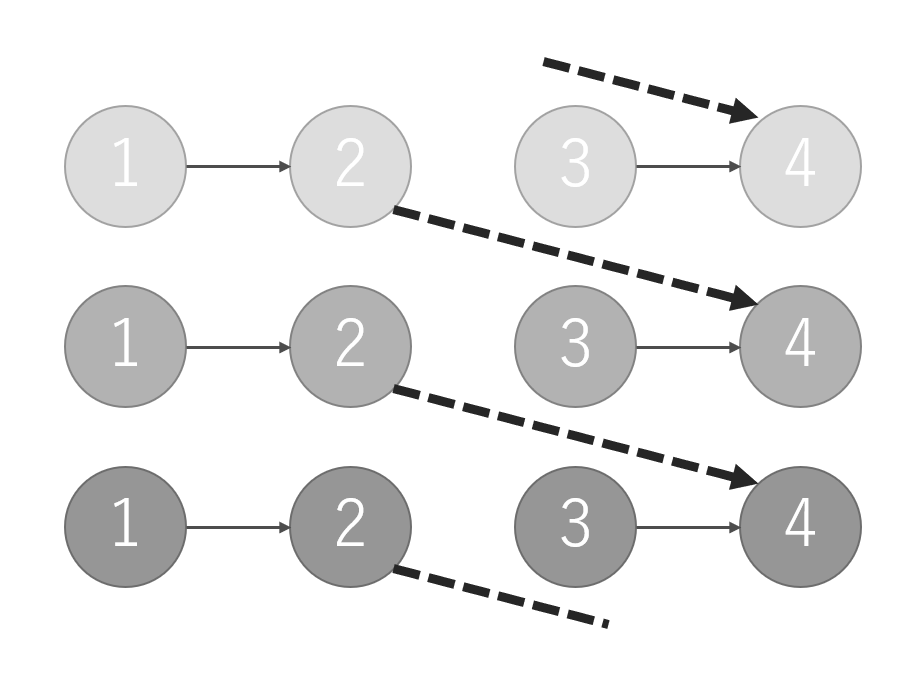
3*Nのノードを持つUnionFindを定義しておいて,$0..N-1$をグループA,$N..2N-1$をグループB,$2N..3N-1$をグループCとすることで同族ならば実線のように,捕食関係にあるならば破線のように互いを結び付けることで,各々の関係を記録することができる.
初心に帰って変分ベイズ(1)::8/31
1. 確率モデルの近似法
確率モデルでは,観測データ${\bf X}$に対するモデルの潜在変数${\bf Z}$の事後分布$p({\bf Z}|{\bf X})$を求めることが目的です.しかしながら,「確率」として取り扱うには総和が1である(=正規化する)必要があります.ベイズの定理においては分母に相当すると言えて, $$ p({\bf Z}|{\bf X})=\frac{p({\bf X}|{\bf Z})p({\bf Z})}{p({\bf X})} $$ というベイズの式から,分母の周辺尤度$p({\bf X})$は分子を$d{\bf Z}$で積分(=周辺化)を行うことで得られて $$ p({\bf X})=\int p({\bf X}|{\bf Z}) p({\bf Z})d{\bf Z} $$ という式になります.
しかしながら,尤度関数($p({\bf X}|{\bf Z})$)事前分布($p({\bf Z})$)がどちらも正規分布などという簡単な条件下では解析的に解けるものの,複雑な一般の問題ではこの計算を行えない場合が多いです. というのも,潜在変数空間の次元数が膨大であったり,積分が閉じた形式*1の解を持たないといったことが主な理由です.
解析的に求まらない問題に対しては何を行うかと言えば,やはり近似です.
よく使われる近似法としては
- マルコフ連鎖モンテカルロ(MCMC)
- 変分ベイズ法(変分推定法)
があり,前者が確率的近似に対して後者が決定的近似です.
MCMCについての詳細は後に述べるとしてそれぞれ以下のような長所と短所が存在します.
| 長所 | 短所 | |
|---|---|---|
| MCMC | $N\rightarrow\infty$ならば厳密解が得られる | 計算量が嵩む |
| 変分ベイズ法 | 計算が少ない | 厳密解は得られない |
変分ベイズ法は複雑な事後分布を分解し近似を行うというスタンスで学習を行います.
その理論の導出の前に,導出の際に用いるKLダイバージェンスについて今だ理解が足りてなかったのでまとめます*2.
2. エントロピーとKLダイバージェンス
2.1. エントロピー
情報学における(離散分布の)エントロピーは以下のように定義でき, $$ I(X)=-\sum_{i}p(i)\log{p(i)} $$ 名の示す通り,統計力学のエントロピーと同様,確率変数$X$の取りうる「乱雑さ」を定量的に表す指標といえます.
例えば,6面体サイコロ$X=[1,2,3,4,5,6]$を考えたとき出目の確率が
- $p(X)=[1/5, 1/10, 1/10, 1/5, 1/5, 1/5]$
- $q(X)=[1/2,1/4,1/8,1/16,1/32,1/32]$
- $r(X)=[1/6,1/6,1/6,1/6,1/6,1/6]$
であるします.
エントロピーはこの場合出目が偏らないほど予測が行いづらいので,いわば出目の予測のしにくさを表す量ともいえます.
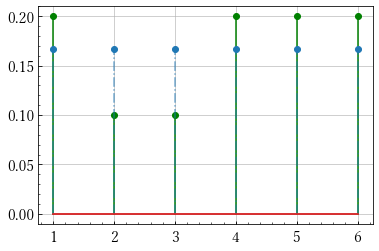
それぞれのエントロピーをpythonで求めてみます.
import numpy as np import matplotlib.pyplot as plt x = np.arange(1,7) q = np.array([1/2, 1/4, 1/8, 1/16, 1/32, 1/32]) p = np.array([1/5, 1/10, 1/10, 1/5, 1/5, 1/5]) r = np.ones(6)/6 # 2つの確率分布を可視化する関数です def plot(p, q): m, s, b = plt.stem(x, p) plt.setp(m, 'color', 'g') plt.setp(s, 'color', 'g') m, s, b = plt.stem(x, q) plt.setp(s, 'linestyle', '-.', 'alpha', 0.6) plt.show() # エントロピーの定義 H = lambda p: -np.sum(p*np.log(p)) print(H(p)) # 1.74806... print(H(q)) # 1.3429... print(H(r)) # 1.79175...
pとrの分布
qとrの分布
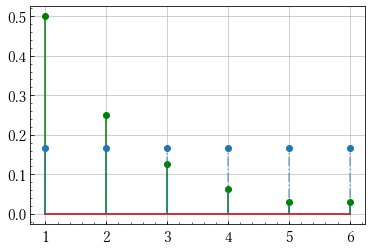
予測通り同様に確からしいサイコロのエントロピーが最も大きいことが分かりました.
また,pとrをみると定義式から見ても明らかですが似た分布ではエントロピーの値が近いことも言えます.
2.2. KLダイバージェンス
二つの確率分布$p,q$に対して距離的な解釈を与えたいとします.すなわち,本来の分布$p$から,実際の分布$q$がどの程度離れているかを考えます.
そこで,下式より定義されるKLダイバージェンスを導入します.
$$ D_{KL}(p||q)=\sum_{i}p_i\log{\frac{p_i}{q_i}} $$
これは変形すると$-p_{i}\log{q_{i}}$と$-p_{i}\log{p_{i}}$の差に分解されるので「$q$に従ってデータが発生したと想定して計算したエントロピー」と「実際に$p$に従って観測されたデータによるエントロピー」の差であると解釈できます*3.
また,定義からもわかるように可換ではありません.
サイコロの例で実際に計算してみると,
D_KL = lambda p, q:np.sum(p*np.log(p/q)) print(D_KL(p, r)) # 0.043692... print(D_KL(r, p)) # 0.048727... print(D_KL(q, r)) # 0.448786...
分布が似ている$p,r$では低い値を取ることが確認できます.
もちろん,KLダイバージェンスは総和を適切に積分に置き換えることで連続な確率変数に対しても適用することが可能です.
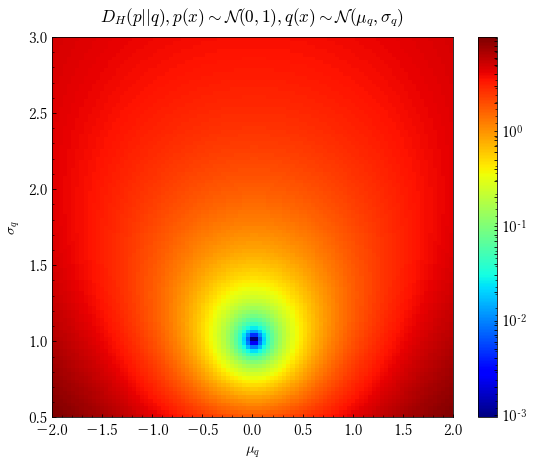
このグラフは$p$が標準正規分布に従い,$q(x)$を$q(x)\sim\mathcal N(x;\mu_{q},\sigma_{q})$として横軸を$\mu_{q}$,縦軸を$\sigma_{q}$としたときのKLダイバージェンスをカラーマップで表したものです.$\mu_{q}=0,\sigma_{q}=1$の際に最も青く表示されていることが見て取れます.
定義からもわかるようにKLダイバージェンスは非負で0となるのは分布が完全に等しいときのみという性質があります.
3. 変分ベイズ
3.1. 変分下界
KLダイバージェンスが分布の類似度を測るものだということが分かりました.なので,確率モデルの事後分布$p({\bf Z}|{\bf X})$を分布$q({\bf Z})$で近似させたいとき, $$ D_{KL}(q({\bf Z})||p({\bf Z}|{\bf X})) $$ を最小化させることでその目的が達成されることが容易にわかるかと思います.
それを踏まえたうえで,モデルの対数周辺尤度$\ln p({\bf X})$(対数周辺尤度はしばしエビデンスと呼ばれます)を考えます.
また,この際一般の期待値に関しイェンセンの不等式が成り立つことを利用します
イェンセンの不等式 $$ f(\mathbb E[X])\leq \mathbb E[f(X)] $$
これを利用して
$$ \begin{eqnarray} \ln p({\bf X})&=&\ln\int p({\bf X},{\bf Z})d{\bf Z}\\ &=&\ln\int p({\bf X},{\bf Z})\frac{q({\bf Z})}{q({\bf Z})}d{\bf Z}\\ &=&\ln\mathbb E_{q}\left[\frac{p({\bf X},{\bf Z})}{q({\bf Z})}\right]\\ &\geq&\mathbb E_{q}\left[\ln\frac{p({\bf X},{\bf Z})}{q({\bf Z})}\right]\\ &=& \int q({\bf Z})\ln\frac{p({\bf X},{\bf Z})}{q({\bf Z})}d{\bf Z} \end{eqnarray} $$
この下界を$\mathcal L(q)$のようにして汎関数を定めます.$\mathcal L$は変分下界と呼ばれ,対数周辺尤度がエビデンスと呼ばれることからELBO(Evidence Lower BOund)と呼ばれます.
さて,つぎに対数周辺尤度からこの変分下界を引いてみます.
$$ \begin{eqnarray} \ln p({\bf X})-\mathcal L(q)&=&\int q({\bf Z})d{\bf Z}\ln p({\bf X})-\int q({\bf Z})\ln\frac{p({\bf X},{\bf Z})}{q({\bf Z})}d{\bf Z}\\ &=&\int q({\bf Z})\ln \frac{q({\bf Z})}{p({\bf Z}|{\bf X})}d{\bf Z}\\ &=&D_{KL}(q({\bf Z})||p({\bf Z}|{\bf X})) \end{eqnarray} $$
とKLダイバージェンスが導き出せます.周辺対数尤度は定数であるので,変分下界の最大化とKLダイバージェンスの最小化は等価であることが分かります.
3.2. 分解による近似分布の計算
上記の式変形で汎関数$\mathcal L(q)$が得られました.ここで,汎関数の極値を求めるにあたってオイラーの方程式*4を使います.
オイラーの方程式
汎関数 $$ I[y]\equiv\int \frac{f(x,y,y')}{q(y)}dx $$
の停留値を求めるには, $$ \frac{\partial f}{\partial y}-\frac{d}{dx}\left(\frac{\partial f}{\partial y'}\right)=0 $$
を解けばよい.
この場合は$y'$が$f$に含まれていないので単に, $$ \frac{\partial f(x,y)}{\partial y(x)}=0 $$
を解けばよいとといえます.
さて,このオイラーの方程式をこのモデルに用いて汎関数である変分下界の極値を求めます.
$q({\bf Z})$を排反な分布に分解して${\bf Z_i}(i=1,2,...,M)$と書くとします.このような分解された形を用いて近似を行うことは物理学の文脈では平均場近似(Mean-Field Approximation)と呼ばれ,特に事後分布をこの方法で近似する方法は変分ベイズ法(Variational Bayes)と呼ばれます.
$$ q({\bf Z})=\prod_{i=1}^{M}q_i({\bf Z_i}) $$
この下では変分下界は $$ \mathcal L(q)=\int \prod_{i=1}^{M}q_{i}({\bf Z_i})\left(\ln p({\bf X},{\bf Z})-\sum_{i=1}^{M}\ln q_{i}({\bf Z}_i)\right)d{\bf Z} $$ と書けます.簡単のために2つの場合を考えることにすると, $$ \mathcal L(q)=\iint q({\bf Z}_1)q({\bf Z}_2)\ln\frac{p({\bf X},{\bf Z})}{q({\bf Z}_1)q({\bf Z}_2)} d{\bf Z}_1d{\bf Z}_2 $$ となります.ここで,$q_2({\bf Z}_2)$を固定して考えると$q_1({\bf Z}_1)$の変分下界は,
$$ \mathcal L(q_1)=\int\left( \int q({\bf Z}_1)q({\bf Z}_2)\ln\frac{p({\bf X},{\bf Z})}{q({\bf Z}_1)q({\bf Z}_2)}d{\bf Z}_1\right)d{\bf Z}_2 $$
と式変形ができることから, $$ f(q_1,{\bf Z}_1)=\int q({\bf Z}_1)q({\bf Z}_2)\ln\frac{p({\bf X},{\bf Z})}{q({\bf Z}_1)q({\bf Z}_2)}d{\bf Z}_1 $$ とすると,変分法が適用でき, $$ \frac{\partial f(q_1,{\bf Z}_1)}{\partial q_1({\bf Z}_1)}=0 $$ を解くことで, $$ \ln q_1({\bf Z}_1)=\int q_2({\bf Z}_2)\ln p({\bf X},{\bf Z})d{\bf Z}_2+\text{const} $$ の時に極値を取ることが分かります. これは $$ \ln q_1^{*}({\bf Z}_1)=\mathbb E_{q_2}[\ln p({\bf X},{\bf Z})]+\text{const} $$ とも解釈できます.
$q_2$も同様, $$ \ln q_2^{*}({\bf Z}_2)=\mathbb E_{q_1}[\ln p({\bf X},{\bf Z})]+\text{const} $$
となります.
さらに,一般の$M$分割に対しても同様のことが言え,同時分布を自分以外の分解された近似分布で期待値を取ることで求めることができます.すなわち,$\mathbb E_{i\neq j}$を$i\neq j$であるすべての${\bf Z}_i$による分布$q_i$の期待値とみなすと $$ \ln q^{*}_{j}=\mathbb E_{i\neq j}[\ln p({\bf X},{\bf Z})]+\text{const} $$ のように最適解が与えられます.
変分ベイズ法はこの式を基礎として近似を行っていきます.$M$分割をおこなうことで$M$個の連立方程式が出来上がります.しかし,その方程式は他の因子$q_i({\bf Z}_i)(i\neq j)$の積分に依存しているので解析的に難しいため,各因子を適当な値で初期化して因子をそれぞれ,他の因子を固定して改良を重ねていくことで学習を行う,という手法がとられます.
4. 変分混合ガウス分布
(編集後記:非常に長くなりそうなので2回くらいに分ける.)
4.1. 事前分布の定義
変分ベイズが適用できる例としてクラスタリング問題が考えられます.
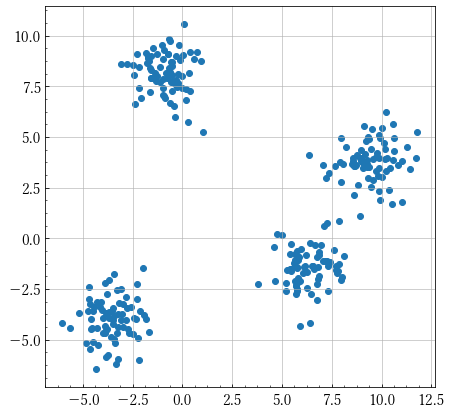
上のような分布に対して何個のクラスタリングに分けられるかという問題を考えるとき,K-Means法やEMアルゴリズムという決定論的な方法が考えられますが,ベイズ法を適用することで,特定のデータのみを説明する縮退が起こりえないことや,最適な要素(コンポーネント,クラスタ)数$K$を交差検証無しに求められるといった利点があります.
確率的なクラスタリングでは,この問題を次のようにモデル化します.
まず各観測値${\bf x}_n$に対して,対応するコンポーネントをOneHot化したベクトル${\bf z}_n$とします.データ数を$N$,コンポーネント数を$K$,次元数を$D$とすると,${\bf X}=\{{\bf x}_1,{\bf x}_2,...,{\bf x}_N\}$は$N\times D$,${\bf Z}=\{{\bf z}_1,{\bf z}_2,...,{\bf z}_N\}$は$N\times K$の行列となります.
ここで,混合ガウス分布は,コンポーネント数が$K$のとき,以下のように線形重ね合わせで表現することができることから,
$$ \sum_{k=1}^{K}\pi_k\mathcal N({\bf x}|{\bf \mu}_k,{\bf \Sigma}_k) $$
のように$\sum \pi_k=1,0\leq\pi_k\leq1$を満たす係数$\pi_k$でその混合比を表現することができます.
${\bf z}_n$はOneHotベクトル化されていることから,分布$p({\bf z}_n)$は, $$ p({\bf z}_n)=\prod_{k=1}^{K}\pi_k^{z_{nk}} $$ のように書き下すこともできます.したがって,分布$p({\bf Z}|{\bf \pi})$,$(\text{where}~{\bf \pi}:=\{\pi_1,\pi_2,...,\pi_k\})$は, $$ p({\bf Z}|{\bf \pi})=\prod_{n=1}^{N}\prod_{k=1}^{K}\pi_k^{z_k} $$ となります.また, $$ p({\bf x}_n|{\bf z}_n)=\prod_{k=1}^{K}\mathcal N({\bf x}_n|{\bf \mu}_k,{\bf \Sigma}_k)^{z_{nk}} $$ となることから,潜在変数が与えられたもとでの観測データのベクトルの条件付き分布は $$ p({\bf X}|{\bf Z},{\bf \mu},{\bf \Lambda})=\prod_{n=1}^{N}\prod_{k=1}^{K}\mathcal N({\bf x}_n|{\bf \mu}_k,{\bf \Lambda}_k^{-1})^{z_{nk}} $$
となります.ただし,共分散行列ではなく精度行列${\bf \Lambda}$(共分散行列の逆行列)を計算の簡単化のために用いています.
次にベイズ的アプローチを導入するため,パラメータ${\bf \pi},{\bf \mu},{\bf \Lambda}$に事前分布を導入します.まず,$p({\bf \pi})$は多変量のベータ分布に相当するディリクレ分布を仮定します*5.
$$ p({\bf \pi})=\frac{\Gamma(\sum \alpha_{0k})}{\prod\Gamma(\alpha_{0k})}\prod_{k=1}^{K}\pi_{k}^{\alpha_{0k}-1} $$ ただし,${\bf \alpha_{0}}$はすべての要素$\{\alpha_{0k}\}$が同じ値のベクトルとした.また上の式の係数はディリクレの正規化定数と呼ばれ,$C({\bf \alpha}_0)$のように表記する.
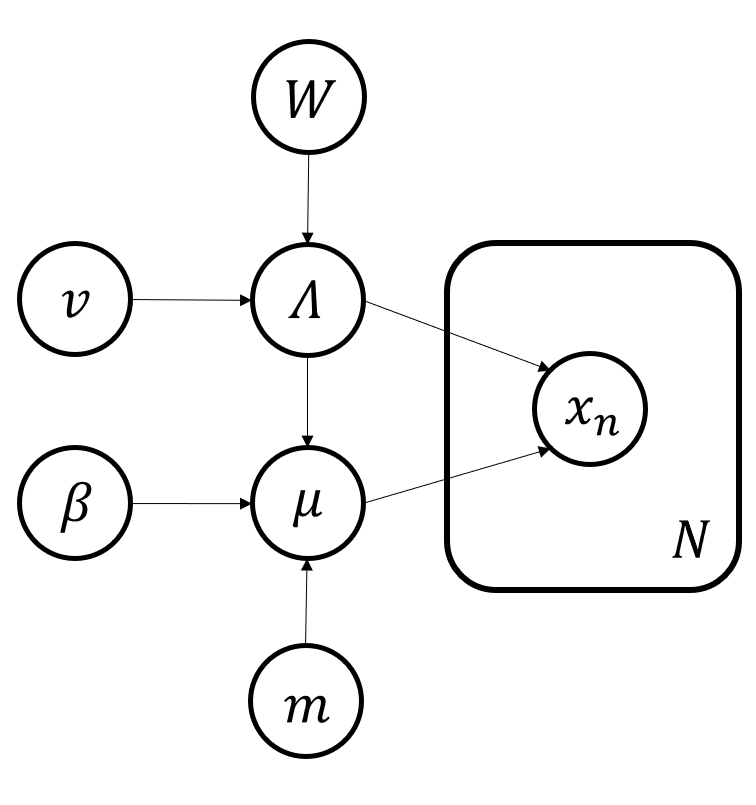
次に分布$p({\bf \mu},{\bf \Lambda})$は,平均と分散が未知なのでガウスウィシャート分布が適します.
$$
p({\bf \mu},{\bf \Lambda})=\prod_{k=1}^{K}\mathcal N({\bf \mu}_k|{\bf m}_0,(\beta_0{\bf \Lambda_k})^{-1})\mathcal W({\bf \Lambda_k}|{\bf W},\nu_0)
$$
(以下ポエム)
残りは次回に回すことにします.この例はPRMLでもなかなか長く歯ごたえのある所だと思うので念入りにやっていきたい.いままでVAEなどについても理解が及ばない点が多く,変分下界の存在意義とかそういったものを理論立てて学べる良い教材だった.
次回
RustでAtcoder Beginner Contest100のD問題を解いた::8/20
高橋君はプロのパティシエになり, AtCoder Beginner Contest 100 を記念して, 「ABC洋菓子店」というお店を開いた.
ABC洋菓子店では, $N$ 種類のケーキを売っている.各種類のケーキには「綺麗さ」「おいしさ」「人気度」の $3$つの値を持ち, $i$種類目のケーキの綺麗さ$x_i$は, おいしさは$y_i$, 人気度$z_i$は である.これらの値は$0$以下である可能性もある. りんごさんは, ABC洋菓子店で$M$個のケーキを食べることにした. 彼は次のように, 食べるケーキの組み合わせを選ぶことにした.
- 同じ種類のケーキを $2$個以上食べない.
- 上の条件を満たしつつ, (綺麗さの合計の絶対値) + (おいしさの合計の絶対値) + (人気度の合計の絶対値) が最大になるように選ぶ.
このとき, りんごさんが選ぶケーキの (綺麗さの合計の絶対値) + (おいしさの合計の絶対値) + (人気度の合計の絶対値) の最大値を求めなさい.
色々と格闘した結果書けたけどこれでいいのか~という気持ちになってる
こんな書き方でいいのか強い方に見てほしいという気持ちになっている.
D問題
use std::cmp::max; use std::fmt::Debug; use std::io::stdin; use std::str::FromStr; fn read<T>() -> Vec<T> where T: FromStr, <T as FromStr>::Err: Debug, { let mut s = String::new(); stdin().read_line(&mut s).unwrap(); s.trim() .split_whitespace() .map(|c| T::from_str(c).unwrap()) .collect() } #[derive(Clone)] struct Review { x: i64, y: i64, z: i64, } impl Review { fn new(r: &[i64]) -> Review { Review { x: r[0], y: r[1], z: r[2], } } fn dot(&self, o: &Review) -> i64 { o.x * self.x + o.y * self.y + o.z * self.z } } fn main() { let x: Vec<usize> = read(); let mut select: Vec<Review> = Vec::new(); for i in 0..8 { let v: Vec<i64> = vec![i & 0x4, i & 0x2, i & 0x1] .iter() .map(|&i| if i == 0 { -1 } else { 1 }) .collect(); select.push(Review::new(v.as_slice())); } let mut reviews: Vec<Review> = Vec::new(); for _ in 0..x[0] { let r: Vec<i64> = read(); reviews.push(Review::new(r.as_slice())); } println!( "{}", select .iter() .map(|sel| { let mut biased_points: Vec<i64> = reviews.iter() .map(|v| v.dot(&sel)) .collect::<Vec<i64>>(); biased_points.sort_by(|a, b| b.cmp(a)); biased_points .iter() .take(x[1]) .fold(0, |sum, item| sum + item) .abs() }) .fold(0, |sum, item| max(sum, item)) ) }
絶対値が最大となる場合であるのでアルゴリズム的には各々の評価指標が負に大きいか正に大きいかを全通り探索($2^{3}=8$通り)すればよい.
しかしまあ,Rustの使い方が全く分からずかなり*1苦戦した.
*1:4時間くらい
Rustを触ってみた::8/19
タイムラインでRustという言語についての話題で盛り上がっていたので試しにABC100のA-C*1を解いてみることにした.
D問題については構造体とtraitやownership関係でイザコザして解けなかった.後程に解答を見て学習してみたいところ.
D問題:
Rustが実際の現場で生かされている具体例などがあれば誰か教えていただきたいです.
チュートリアルとしては
https://doc.rust-jp.rs/the-rust-programming-language-ja/1.6/book/getting-started.html
を使っています.
A問題
use std::fmt::Debug; use std::io::stdin; use std::str::FromStr; fn read<T>() -> Vec<T> where T: FromStr, <T as FromStr>::Err: Debug, { let mut s = String::new(); stdin().read_line(&mut s).unwrap(); s.trim() .split_whitespace() .map(|c| T::from_str(c).unwrap()) .collect() } fn main() { let input: Vec<u32> = read(); println!( "{}", match &input.into_iter().find(|&v| v > 8) { Some(_v) => ":(", _ => "Yay!", } ) }
行ごとの標準入力は
を参照しました.
アルゴリズムは所有権とかのノウハウがいまだにつかめない.
into_iterとfoldやfindが競プロにおいてはかなり使い勝手がいいと感じる.
B問題
use std::fmt::Debug; use std::io::stdin; use std::str::FromStr; fn read<T>() -> Vec<T> { ... } fn main() { let x: Vec<u32> = read(); println!( "{}", match x[1] { 100 => (x[1] + 1) * 100u32.pow(x[0]), _ => x[1] * 100u32.pow(x[0]), } ); }
全探索などを使わずとも,簡単なことに気付けばAより簡単な問題でした.
C問題
use std::fmt::Debug; use std::io::stdin; use std::iter::Iterator; use std::str::FromStr; fn read<T>() -> Vec<T> { ... } fn main() { let _n: Vec<u32> = read(); let a: Vec<u32> = read(); println!( "{:?}", a.into_iter().fold(0, |mut sum, mut v| { while v & 0x1 == 0 { v >>= 1; sum += 1 } sum }) ); }
- 3で掛けることは動作に関して全く影響しない
- 全て2で割る動作ができないが結局のところ最も多くの手数を稼ぐには一つだけ2で割る動作のみをすればいい
- したがって,各要素が2で割れる回数の総和を取ればよい
- foldがかなり便利だった.
初心に帰ってベイズ線形多項式回帰(2):エビデンス近似編::8/15
エビデンス近似
先日の記事日記(8/5):初心に帰ってベイズ線形多項式回帰(1) - 日記帳では,線形回帰に対してベイズ的な取り扱いを導入しましたが,ハイパーパラメータにあたる$\alpha,\beta$をあらかじめ決める必要があり,完全にベイズ的な取り扱いである回帰モデルとはいえないので,このハイパーパラメータに事前分布を設けることで,線形回帰モデルを完全にベイズ的に扱うことを考えることにします.
ベイズ多項式回帰の復習
多項式の係数に当たる${\bf w}$に対してガウス分布に従う事前分布を導入し,ベイズ的な取り扱いをすることを考えます. $$ p({\bf w})=\mathcal N({\bf w}|0,\alpha^{-1}I) $$
次に事後分布$p({\bf w}|{\bf t})$を求めるため,尤度関数を求めます. $$ \Phi= \left[ \begin{array}{cccc} \phi_0(x_{1})&\phi_{1}(x_{1})&\cdots & \phi_{M -1}(x_{1})\\ \phi_0(x_{2})&\phi_1(x_{2})&\cdots&\phi_{M -1}(x_{2})\\ \vdots&\vdots&\ddots&\vdots\\ \phi_0(x_{N})&\phi_1(x_{N})&\cdots&\phi_{M -1}(x_{N})\\ \end{array} \right]= \left[ \begin{array}{cccc} x_{1}^{0}&x_{1}^{1}&\cdots & x_{1}^{M -1}\\ x_{2}^{0}&x_{2}^{1}&\cdots & x_{2}^{M -1}\\ \vdots&\vdots&\ddots&\vdots\\ x_{N}^{0}&x_{N}^{1}&\cdots & x_{N}^{M -1}\\ \end{array} \right] $$ のように定めることで,尤度関数は
$$ E({\bf w})=\mathcal N({\bf t}| \Phi {\bf w},\beta^{-1}I) $$ のように書き表せます*1.
したがって,事後分布はガウス分布で表すことができ,ベイズの定理から $$ \begin{eqnarray} p({\bf w}|\Phi,\alpha,\beta,{\bf t})&=&\frac{E({\bf w})\mathcal N({\bf w}|0,\alpha^{-1}I)}{p({\bf t}|\Phi,\alpha,\beta)}\\ &=&\mathcal N({\bf w}|{\bf m}_N,{\bf S}_N)\\ &\text{where}&~~{\bf m}_N=\beta {\bf S}_N\Phi^{T}{\bf t},{\bf S}_N^{-1}=\alpha I+\beta\Phi^{T}\Phi \end{eqnarray} $$
ここで,事後分布の対数を取ると $$ \ln p({\bf w}|\Phi,\alpha,\beta,{\bf t})=-\frac{\beta}{2}\sum^{N}_{n=1}(t_n-{\bf w}^{T}\phi({\bf x})_n)^{2}-\frac{\alpha}{2}{\bf w}^{T}{\bf w}+\text{Const} $$ となり,うまい具合に二乗和誤差項と正則化項が現れていることがわかります.
このとき,入力${\bf x}$に対する$t$の予測確率分布は $$ p(t|{\bf t},\alpha, \beta)=\int p(t|{\bf w},\beta)p({\bf w}|{\bf t},\alpha,\beta)\text{d}{\bf w} $$ を評価すればよく, $$ p(t|{\bf t},\alpha, \beta)=\mathcal N\left(t\bigg|{\bf m}_N\phi({\bf x}),\frac{1}{\beta}+\phi({\bf x})^{T}{\bf S}_N\phi({\bf x})\right) $$ のように計算されます.
ここで,$N \rightarrow \infty$の極限を考えると,分散の第二項は0に近づき,加法性ノイズ$\beta$にのみ依存することが分かります.すなわち,サンプル数を無限に近づけるにしたがって,ベイズ推定の結果は最尤推定の結果に近づくことが分かるかと思います.
エビデンス近似
ハイパーパラメータに対しても,事前分布を設け,ベイズ的に取り扱うことを考えます. ハイパーパラメータに対して,事前分布を設けると,予測分布は以下のように与えられます. $$ p(t|{\bf t})=\iiint p(t|{\bf w},\beta)p({\bf w}|{\bf t},\alpha,\beta)p(\alpha,\beta|{\bf t})\text{d}{\bf w}\text{d}\alpha\text{d}\beta $$
それぞれ,$p(t|{\bf w},\beta)$は,ガウスノイズ$\beta$下の予測値の分布,$p({\bf w}|{\bf t},\alpha,\beta)$は事後分布に等しい.$p(\alpha,\beta|{\bf t})$を考えると,ベイズの定理から, $$ p(\alpha,\beta|{\bf t})\propto p({\bf t}|\alpha,\beta)p(\alpha,\beta) $$ となります.ここの$p({\bf t}|\alpha,\beta)$がエビデンス関数と呼ばれるものです.エビデンス関数は,${\bf w}$に対しての周辺化*2で得られ, $$ E({\bf w})=\frac{\beta}{2}||{\bf t}-\Phi{\bf w}||_{2}^{2}+\frac{\alpha}{2}{\bf w}^{T}{\bf w} $$ を用いて, $$ p({\bf t}|\alpha,\beta)=\left(\frac{\beta}{2\pi}\right)^{N/2}\left(\frac{\alpha}{2\pi}\right)^{M/2}\int \exp{-E({\bf w})}\text{d}{\bf w} $$ となります.ただし,$M$は${\bf w}$の次元数です.
計算過程はPRMLを参照するとして,対数エビデンス関数は結果以下のようになります. $$ \ln p({\bf t}|\alpha,\beta)=\frac{M}{2}\ln\alpha+\frac{N}{2}\ln\beta-E({\bf m}_N)-\frac{1}{2}\ln|A|-\frac{N}{2}\ln(2\pi) $$ ただし, $$ A=\alpha I+\beta \Phi^{T}\Phi $$ です.このエビデンス関数を最大化する$\alpha,\beta$を求めることは,その定義からトレーニングデータ${\bf t}$を最も生成しやすいハイパーパラメータの値を求めることに等しく,交差検証を使わずとも最もよいハイパーパラメータの値を求めることができます.
エビデンス関数の最大化
詳しい導出はPRMLを参照するとして,以下のように更新を続けることで,最適値推定を行います.
- $\displaystyle \alpha,\beta$をまず適当な値で初期化する.
- $\beta \Phi^{T}\Phi$の固有値を$\lambda_{i}$として,$\displaystyle \gamma:=\sum_{i}\frac{\lambda_{i}}{\alpha+\lambda_{i}}$を計算する.
- $\gamma$と${\bf m}_N$から,$\alpha$を$\displaystyle\alpha=\frac{\gamma}{{\bf m}_N^{T}{\bf m}_N}$で更新する.
- データ$x_i,t_i$から,$\beta$を$\displaystyle \beta^{-1}=\frac{1}{N-1}\sum_{n=1}^{N}(t_n-{\bf m}_N^{T}\phi(x_n))^{2}$で更新する
- $\alpha,\beta$が収束するまで2.から4.を繰り返す.
これを実装してみることにします.
実装
class BayesLinearPolynomialRegression(object): def __init__(self, M=3, alpha=1e-2, beta=1): self.M = M self.alpha = alpha self.beta = beta def polynomialize(self, x): phi = np.array([x**i for i in range(self.M + 1)]).T return phi def fit(self, X, t): phi = self.polynomialize(X) self.w_s = np.linalg.inv(self.alpha * np.eye(phi.shape[1]) + self.beta * phi.T.dot(phi)) self.w_m = self.beta * self.w_s.dot(phi.T.dot(t)) def predict(self, x): phi = self.polynomialize(x) t_m = phi.dot(self.w_m) t_v = 1/self.beta + np.sum(phi.dot(self.w_s) * phi, axis=1) t_s = np.sqrt(t_v) return t_m, t_v class BayesLinearPolynomialRegressionWithEvidence( BayesLinearPolynomialRegression): def __init__(self, M, alpha, beta, iter_num=100): super(BayesLinearPolynomialRegressionWithEvidence, self).__init__( M=M, alpha=alpha, beta=beta) self.iter_num = iter_num self.isnan = False def fit_1(self, X, t): phi = self.polynomialize(X) lamb, u = np.linalg.eig(self.beta * phi.T.dot(phi)) lamb = lamb.real self.gamma = np.sum(lamb / (self.alpha + lamb)) self.w_s = np.linalg.inv(self.alpha * np.eye(phi.shape[1]) + self.beta * phi.T.dot(phi)) self.w_m = self.beta * self.w_s.dot(phi.T).dot(t) self.alpha = self.gamma / (self.w_m.T.dot(self.w_m)) N = t.shape[0] self.beta = (N - self.gamma) / (np.sum( np.square(t - phi.dot(self.w_m)))) if np.isinf(self.alpha) or np.isnan(self.alpha) or np.isinf(self.beta): if not self.isnan: self.isnan = True print("[W] alpha or beta value is inf") return Emn = 0.5*self.beta*np.sum(np.square(t - phi.dot(self.w_m))) +\ 0.5*self.alpha*self.w_m.T.dot(self.w_m) A = self.alpha * np.eye(self.w_m.shape[0]) + self.beta * phi.T.dot(phi) detA = np.linalg.det(A) if np.isinf(detA): if not self.isnan: self.isnan = True print("[W] |A| is inf") return self.evidence = 0.5*self.M*np.log(self.alpha)+0.5*N*np.log(self.beta)-\ Emn-0.5*np.log(detA)-\ 0.5*N*np.log(2*np.pi) def fit(self, X, t): for i in range(self.iter_num): self.fit_1(X, t) if self.isnan: print("[W] fit may failed") return
実装コードすべてはPRML/notes/BayesRegression.ipynb · GitHubを参照してください.
予測分布の算出はエビデンス近似を行わないベイズ線形回帰と全く同じであるので継承を用いています.
結果
🍤デンス近似(パラメータのαとβうまく求めてくれるらしい) pic.twitter.com/W0vPxHggRT
— ツナ缶 (@fujifog) 2018年8月5日
近似の様子を一回の更新ごとにアニメーションとしています.
雲は流れてhttps://t.co/ogCJnWYrnl pic.twitter.com/ONqAkBMAQG
— ツナ缶 (@fujifog) 2018年8月5日
Mを1から14まで変えたときの対数エビデンス値の変化を求めています.
くぅ~疲れましたw これにて完結です!
実は、部室に行ったらPRMLが本棚にあったのが始まりでした
本当は話のネタなかったのですが←
やる気を無駄にするわけには行かないので流行りのベイズで挑んでみた所存ですw
以下、パラメタ達のみんなへのメッセジをどぞ
$\alpha$「みんな、見てくれてありがとう ちょっと腹黒なところも見えちゃったけど・・・気にしないでね!」
$\beta$「いやーありがと! 私のかわいさは二十分に伝わったかな?」
$\gamma$「見てくれたのは嬉しいけどちょっと恥ずかしいわね・・・」
$p({\bf t}|\alpha,\beta)$「見てくれありがとな! 正直、作中で言った私の気持ちは本当だよ!」
$|A|$「・・・ありがと」Singular Matrix...
では、
$\alpha,\beta,\gamma,p({\bf t}|\alpha,\beta),|A|$,俺「皆さんありがとうございました!」
終
$\alpha,\beta,\gamma,p({\bf t}|\alpha,\beta),|A|$「って、なんで俺くんが!? 改めまして、ありがとうございました!」
本当の本当に終わり
RVMとRails::8/11
| 時刻 | したこと |
|---|---|
| 10:00 | 起床 |
| 14:00 | PRML7章 |
| 17:00 | Rails環境構築 |
関連ベクトルマシン(RVM)
関連ベクトルマシン(RVM)
— ツナ缶 (@fujifog) 2018年8月11日
ガウス過程と似た方法で,重みパラメータが無限大に発散することによってそのパラメータの事後分布を0近辺に集中させることで疎性が高いモデルを得る手法らしい.
SVMと比較して計算量は掛かるけど,ハイパーパラメータを自動推定してくれるので割と使えそう pic.twitter.com/9fh9QyaHVK
SVMの章で出てきたけどやってることは上巻3章の回帰とあんま変わってない気がする.単に,重みの共分散が「スカラー値×単位行列」を「対角行列」に変えただけというイメージ.
Rails
このサイトを再度3章から読んでいきます.
進捗を共有できる進捗ノートです.
ただ単に進捗を報告するのではなく,期日を設けてスケジュールを立てる機能だとか,プロジェクト単位での質問のほかに,質問BOXの作成なども行える神ツールです.つかおうね!!
::8/10
| 日 | やったこと |
|---|---|
| 8/07 | ベイズ線形回帰のエビデンス近似 |
| 8/08 | ガウス過程の学習と実装(PRML) |
| 8/09 | 休息の日とarchive |
| 8/10 | GPとNNとarXiv |
PRMLを6章まで読み進めた.理解はまだできていない.
8/9はCiv5を終始やってた.ちょっと30分やる予定だったが,気付いたら8時間くらいやってた.
8/7
🍤デンス近似(パラメータのαとβうまく求めてくれるらしい) pic.twitter.com/W0vPxHggRT
— ツナ缶 (@fujifog) 2018年8月5日
8/8
ガウス過程 pic.twitter.com/Izb3bADfJv
— ツナ缶 (@fujifog) 2018年8月8日
8/9
某委員長系某チューバーの某とCiv5
8/10
進捗まとめ
最終更新:2018/08/10
書籍
機械学習

Python機械学習プログラミング 達人データサイエンティストによる理論と実践 (impress top gear)
- 作者: Sebastian Raschka,株式会社クイープ,福島真太朗
- 出版社/メーカー: インプレス
- 発売日: 2016/06/30
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (4件) を見る
Pythonの文法とSklearnの使い方,古典的な機械学習アルゴリズム(パーセプトロンや,主成分分析,SVMなど)を学習した,理論と実装が程よい比率で載っており,全くPythonに触れたことがない人でも結構楽に読み進められる.

ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
- 作者: 斎藤康毅
- 出版社/メーカー: オライリージャパン
- 発売日: 2016/09/24
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (18件) を見る
とりあえずイチから作ってみたくなって購入.あまり触れていないがとても読み進めやすく講習会でも結構有効活用できた.誤差逆伝搬のリンゴに税金がかかるところによる例示がいまいち理解できなかった.

- 作者: Ian Goodfellow,Yoshua Bengio,Aaron Courville,岩澤有祐,鈴木雅大,中山浩太郎,松尾豊,味曽野雅史,黒滝紘生,保住純,野中尚輝,河野慎,冨山翔司,角田貴大
- 出版社/メーカー: KADOKAWA
- 発売日: 2018/03/07
- メディア: 単行本
- この商品を含むブログ (1件) を見る
かなり骨があり,なかなか読み進められないが深層学習に関する網羅系の本の中では間違いなく圧倒的な網羅度を誇っているかと思う.

- 作者: C.M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
- 出版社/メーカー: 丸善出版
- 発売日: 2012/04/05
- メディア: 単行本(ソフトカバー)
- 購入: 6人 クリック: 33回
- この商品を含むブログ (20件) を見る

- 作者: C.M.ビショップ,元田浩,栗田多喜夫,樋口知之,松本裕治,村田昇
- 出版社/メーカー: 丸善出版
- 発売日: 2012/02/29
- メディア: 単行本
- 購入: 6人 クリック: 14回
- この商品を含むブログを見る
現在進行形で読んでいる.

- 作者: Francois Chollet,巣籠悠輔,株式会社クイープ
- 出版社/メーカー: マイナビ出版
- 発売日: 2018/05/28
- メディア: 単行本(ソフトカバー)
- この商品を含むブログ (2件) を見る
某弊大学サークルから借りた代物.実装がたくさんでうれしい.
論文読書
#2 An Introduction to Image Synthesis with Generative Adversarial Nets - HackMD
[GAN]GANの応用とかを学びたくて読んだ.リンクをたどって色々見た.
#3 Improved Training of Wasserstein GANs - HackMD
[GAN]勾配に対して罰則を設けたワッシャーシュタイン距離で誤差を記述するGAN
#6 Improved Techniques for Training GANs - HackMD
[GAN]GANの小手先テクニック.いずれ実装したい.
#8 Self-Attention Generative Adversarial Networks - HackMD
[GAN]Attentionに対する前提知識を得てから読むべきだった感がある
#9 Spectral Normalization for Generative Adversarial Networks - HackMD
[GAN]L2ノルムで割ってパラメータの発散を抑える手法
#10 Auto-Encoding Variational Bayes - HackMD
[VAE]VAEという単語が初めて出てきたやつ
#13 Deep Neural Networks as Gaussian Processes - HackMD
[Bayes]GP+DNN
実装
Pythonの練習用に書いたマルコフ連鎖による単純な文章生成.
Winでも動かしたくてJanomeで書き換えただけのヤツ
倒立振子のシミュレーションと強化学習(Q-学習)
講習会用に拵えた各種オプティマイザの挙動の可視化
単純なVAEのKerasによる実装
PRML/notes/BayesRegression.ipynb · GitHub
PRML3章のベイズ回帰の簡単な実装
PRML/notes/GaussianProcess.ipynb · GitHub
PRML6章のガウス過程回帰の単純な実装
SpectralNormDCGAN-Torch.ipynb · GitHub
写経.torchの学習をしたかった.
ロジスティック関数のカオス
初心に帰ってベイズ線形多項式回帰(1)::8/5
| 時刻 | 行動 |
|---|---|
| 10:00 | 起床 |
| 13:00 | 外出 |
| 17:00 | 読書など |
ベイズ線形回帰
おとといの記事日記(8/2):初心に帰って回帰分析 - 日記帳では,線形回帰モデルのパラメータを最尤推定というアプローチで決めた.
しかしながら,このモデルでは過学習を抑えるために正則化項というパラメータを設ける必要があった.そこで,ベイズ的な手法を導入することで,過学習を抑えることができ,なおかつモデルのパラメータ数がデータ数より多くなっても問題ないようだ.
解説の前にガウス分布は以下の法則を満たすことを紹介する.
[A]
${\bf x}$の周辺分布と${\bf x}$が与えられた際の${\bf y}$の条件付き分布が
$$ p({\bf x})=\mathcal N({\bf x}|\mu, \Lambda^{-1}) $$ $$ p({\bf y}|{\bf x})=\mathcal N({\bf y}|A{\bf x}+b,L^{-1}) $$
として与えられるとき,${\bf y}$の周辺分布と${\bf y}$が与えられた際の${\bf x}$の条件付き分布は
$$ p({\bf y})=\mathcal N({\bf y}|A\mu +b,L^{-1}+A\Lambda^{-1}A^{-1}) $$ $$ p({\bf x}|{\bf y})=\mathcal N({\bf x}|\Sigma(A^{T}L({\bf y}-b)+\Lambda \mu),\Sigma) $$ となる.ただし,$\Sigma=(\Lambda+A^{T}LA)^{-1}$である.
回帰モデルの尤度関数は入力$X$,目標${\bf t}$,基底関数$\phi(\cdot)$,精度$\beta=\sqrt{\sigma}^{-1}$に対し, $$ p({\bf t}|X,{\bf w},\beta)=\prod_{n=1}^{N}\mathcal N(t_n|{\bf w}^{T}\phi({\bf x}),\beta^{-1}) $$ と与えられることから,共役事前分布*1は
$$ p({\bf w})=\mathcal N({\bf w}|m_0,S_0) $$
のように書くことができる.
上で紹介した式変形[A]を使えば,事後分布$p({\bf w}|{\bf t})$は $$ p({\bf w}|{\bf t})=\mathcal N({\bf w}|m_N,S_N) $$ $$ m_N=S_N(S_0^{-1}m_0+\beta\Phi^{T}{\bf t}),S_N^{-1}=S_0^{-1}+\beta\Phi^{T}\Phi $$ $$ \Phi= \left[ \begin{array}{cccc} \phi_0(x_{1})&\phi_{1}(x_{1})&\cdots & \phi_{M -1}(x_{1})\\ \phi_0(x_{2})&\phi_1(x_{2})&\cdots&\phi_{M -1}(x_{2})\\ \vdots&\vdots&\ddots&\vdots\\ \phi_0(x_{N})&\phi_1(x_{N})&\cdots&\phi_{M -1}(x_{N})\\ \end{array} \right] $$ となる.また,ガウス分布は最頻値と期待値が一致するので,事後分布を最大化させる重み${\bf w}_{MAP}$は単に${\bf w}_{MAP}=m_N$である.
ここで,事前分布を簡単のために $$ p({\bf w}|\alpha)=\mathcal N({\bf w}|0,\alpha^{-1}I) $$ として与える.このとき,$m_N,S_N$は $$ m_N=\beta S_N\Phi^{T}{\bf t},S_N^{-1}=\alpha I+\beta\Phi^{T}\Phi $$ となる.
ここで,事後分布の対数を取ると $$ \ln p({\bf w}|{\bf t})=-\frac{\beta}{2}\sum^{N}_{n=1}(t_n-{\bf w}^{T}\phi({\bf x})_n)^{2}-\frac{\alpha}{2}{\bf w}^{T}{\bf w}+\text{Const} $$ となり,この関数の${\bf w}$に関する最大化は二乗和誤差と正則化項の和の最小化に一致することに等価であることが分かる.
このとき,入力${\bf x}$に対する$t$の予測確率分布は $$ p(t|{\bf t},\alpha, \beta)=\int p(t|{\bf w},\beta)p({\bf w}|{\bf t},\alpha,\beta)\text{d}{\bf w} $$ を評価すればよく, 条件付き分布が $$ p(t|{\bf x},{\bf w},\beta)=\mathcal N(t|m_N\phi({\bf x}),\beta^{-1}) $$ で,事後分布が上のように与えられていることから式変形[A]から,予測分布は $$ p(t|{\bf t},\alpha, \beta)=\mathcal N\left(t\bigg|m_N\phi({\bf x}),\frac{1}{\beta}+\phi({\bf x})^{T}S_N\phi({\bf x})\right) $$ として与えられる.
データから最適な$\alpha,\beta$を決める方法は,後日に紹介,実装するとして,まずはこのベイズ線形回帰モデルをPythonで実装する.
実装
import numpy as np import matplotlib.pyplot as plt class BayesLinearPolynomialRegression(object): def __init__(self, M=3, alpha=1e-2, beta=1): self.M = M self.alpha = alpha self.beta = beta def polynomialize(self, x): phi = np.array([x**i for i in range(self.M + 1)]).T return phi def fit(self, X, t): phi = self.polynomialize(X) self.w_s = np.linalg.inv(self.alpha * np.eye(phi.shape[1]) + self.beta * phi.T.dot(phi)) self.w_m = self.beta * self.w_s.dot(phi.T.dot(t)) def predict(self, x): phi = self.polynomialize(x) t_m = phi.dot(self.w_m) t_v = 1/self.beta + np.sum(phi.dot(self.w_s) * phi, axis=1) t_s = np.sqrt(t_v) return t_m, t_v
polynomializeメソッドはサンプル点集合${\bf x}={x_n}$に基底関数を施し,以下のように定義される$\Phi$を生成するメソッドである*2
今回は多項式基底関数を用いたため,最右辺のような行列を生成する. $$ \Phi= \left[ \begin{array}{cccc} \phi_0(x_{1})&\phi_{1}(x_{1})&\cdots & \phi_{M -1}(x_{1})\\ \phi_0(x_{2})&\phi_1(x_{2})&\cdots&\phi_{M -1}(x_{2})\\ \vdots&\vdots&\ddots&\vdots\\ \phi_0(x_{N})&\phi_1(x_{N})&\cdots&\phi_{M -1}(x_{N})\\ \end{array} \right]= \left[ \begin{array}{cccc} x_{1}^{0}&x_{1}^{1}&\cdots & x_{1}^{M -1}\\ x_{2}^{0}&x_{2}^{1}&\cdots & x_{2}^{M -1}\\ \vdots&\vdots&\ddots&\vdots\\ x_{N}^{0}&x_{N}^{1}&\cdots & x_{N}^{M -1}\\ \end{array} \right] $$
fit及びpredictは,上記の数式を愚直に実装すればよいのだが,predictにおいて複数の点を予測するため,$\phi$に対してではなく$\Phi$に対する予測をさせるため若干の式変形を行う.その際,内積が要素積の総和で表されることを利用する.
def sin(x): return np.sin(2*np.pi*x) def generate_data(func, noise_scale, N): x = np.random.uniform(size=N) t = func(x) + np.random.normal(scale=noise_scale, size=x.shape) return x, t def display_predict(truefunc, X_train, t_train, X_test, t_test_m, t_test_s,text=None,name=None): fig = plt.figure(figsize=(8,6)) plt.fill_between(X_test, t_test_m-t_test_s, t_test_m+t_test_s,color='r',alpha=0.25) plt.plot(X_test, truefunc(X_test), label='Target Curve', c='blue') plt.scatter(X_train, t_train, facecolors='none', edgecolors='black', label='Observated Points', alpha=0.6) plt.plot(X_test, t_test_m, c='r', label='Predict Curve') if text is not None: plt.title(text) plt.xlabel('$x$') plt.ylabel('$t$') plt.legend() plt.ylim((-1.5,1.5)) if name is not None: plt.savefig('{}.png'.format(name)) plt.close() else: plt.show()
補助関数を定義する.上から,目的曲線関数,データ生成関数,グラフ表示関数である.display_predictの引数はそれぞれ実曲線,訓練データX軸,訓練データt軸,テストデータX軸,テストデータt軸の平均,標準偏差...である. この関数を実行すると下記のような,$\pm \sigma$の範囲が赤く塗られた図が生成される.

X_train, t_train = generate_data(sin, 0.15,60) model = BayesLinearPolynomialRegression(M=20, alpha=1e-3, beta=5) model.fit(X_train, t_train) X_test = np.linspace(0,1,200) t_m, t_s = model.predict(X_test) display_predict(sin, X_train, t_train, X_test, t_m, t_s)
データ数,$\alpha,\beta$を変えた際の予測の変化の様子は以下のようになる.
たしかに,$\alpha$が正則化係数として,$\beta$が制度の範囲を制御するパラメータとして働いていることが分かる.
次はエビデンス近似をまとめたい
*1:尤度をかけて事後分布を求めると、その関数形が同じになるような事前分布のこと.参照:【ベイズ統計】共役事前分布とは?わかりやすく解説 | 全人類がわかる統計学
初心に帰って回帰分析::8/2
| 時刻 | 行動 |
|---|---|
| 11:00 | 起床 |
| 14:00 | 帰省開始 |
| 15:00 | 日吉駅発 |
| 18:00 | 土浦駅着 |
| 22:00 | PRML読書 |
帰省するだけで結構疲れて辛いものがある.
PRML
1.1. 例:多項式曲線フィッティング
ベイズ理論ばっかり載ってるイメージのPRMLだけど最初の数ページは普通の回帰分析の例が載ってる. なので,折角ならと復習がてら回帰分析をイチから実装してみる.
回帰分析とは
そもそも回帰分析とは与えられた入力ベクトルから,目標値
の値を予測する問題だ.すなわち,
と入力と出力の関係を表した時の関数
はどのように書けるかを求める問題といえる.
とりわけ,
のようにに関して線形になっているような回帰モデルのことは線形回帰モデルと呼ばれている.
しかしながら,こういったモデルは入力に関しても線形であるため,表現能力に乏しいという欠点がある.
そこで,入力ベクトルに対して,非線形な関数を施してやることで,このモデルを以下のように拡張する(
に関して線形なのでこれも線形回帰モデル!!!).
ただし,である.この項は,関数の切片にあたるバイアス項である.
sinを多項式でフィッティングさせよう
今回は以下のようなsinに沿った値に対しノイズを加えた値を上記の例で
とした場合,すなわち
次多項式
で入力と目標値との関係をモデル化する.

ただし,は設計者が任意に定めるパラメータである.
次に,このモデルにより予想された多項式曲線と目標値とのずれを定量化させる.こうすることで最適曲線の導出はこの関数の最小化により達成されることとなる.
この定量的なずれは誤差関数と呼ばれ,単純でかつよく用いられているものの例として二乗和誤差がある.このモデルの二乗和誤差は次式にて定義される.
これは,例えば曲線が次のように予測されたときの

距離の総和に等しい(下図中の紫線の和)

なお,誤差に1/2が掛けられているのは単に後々計算しやすくするためである*1.
ここで,個のデータをまとめて処理するため,以下のように行列としてデータを扱うことにする.
$$ \Phi= \left[ \begin{array}{cccc} \phi_0(x_{1})&\phi_{1}(x_{1})&\cdots & \phi_{M -1}(x_{1})\\ \phi_0(x_{2})&\phi_1(x_{2})&\cdots&\phi_{M -1}(x_{2})\\ \vdots&\vdots&\ddots&\vdots\\ \phi_0(x_{N})&\phi_1(x_{N})&\cdots&\phi_{M -1}(x_{N})\\ \end{array} \right]= \left[ \begin{array}{cccc} x_{1}^{0}&x_{1}^{1}&\cdots & x_{1}^{M -1}\\ x_{2}^{0}&x_{2}^{1}&\cdots & x_{2}^{M -1}\\ \vdots&\vdots&\ddots&\vdots\\ x_{N}^{0}&x_{N}^{1}&\cdots & x_{N}^{M -1}\\ \end{array} \right] , {\bf t}= \left[ \begin{array}{c} t_{1}\\ t_{2}\\ \vdots\\ t_{N}\\ \end{array} \right] $$
すると二乗和誤差は以下のように表すことができる.
$$ E({\bf w})=\frac{1}{2}||\Phi{\bf w}-{\bf t}||_{2}^{2} $$
これの微分値が0となる点が最小(凸性より)なので,ちょちょっと計算すると,
$$ {\bf w}^{*}=(\Phi^{T}\Phi)^{-1}\Phi^{T}{\bf t} $$
のときに最小値をとることがわかる.
以下,この単純なモデルを実装する.
単純な線形回帰の実装
import numpy as np import matplotlib.pyplot as plt def generate_data(noise_scale, N): X_train = np.linspace(0, 1, N) t_train = np.sin(2*np.pi* X_train) + np.random.normal(scale=noise_scale,size=(N,)) return X_train, t_train def display_data(funcs, X, t,y_lim=(-1.4, 1.4),name=None,title=None): fig = plt.figure(figsize=(7,5)) x = np.linspace(X.min(), X.max(), 200) plt.ylim(y_lim) if title is not None: plt.title(title) for func in funcs: plt.plot(x, func(x)) plt.scatter(X, t, facecolors='none', edgecolors='r') if name is not None: plt.savefig("{}.png".format(name)) else: plt.show() plt.close()
補助関数は,データ生成関数と画像の表示関数である.display_dataのfuncsにはfunctionのlistを渡す.
X_train, t_train = generate_data(0.3, 10) X_test, t_test = generate_data(0.3, 30) class SimpleMSE(): def __init__(self,X_train, t_train): self.X_in = X_train self.t = t_train def fit(self, M=4,ndiv = 500): self.M = M phi = np.empty((self.X_in.shape[0],self.M)) for i, col in enumerate(phi.T): phi[:,i] = self.X_in**i theta = np.linalg.solve(phi.T.dot(phi), phi.T.dot(self.t)) func = lambda x: sum([th * x**i for i, th in zip(range(self.M), theta)]) return theta, func
numpyには$Ax=b$に対して$x=A^{-1}b$を一発で求めるnp.linalg.solve(A, b)という関数があるのでそれで
重みを求める.
$M $をいろいろ変えた場合結果は以下のようになる.
$M=2$

$M=3$

$M=4$

$M=10$

$M=4$でいい感じに近似できているのに対し,$M=10$では入力画像に対して適合しすぎている. このような場合汎化性能*2としては低い.このような状態を過適合だとか過学習だとかいう.
過学習の防止方法
ここで,$M=4$の場合と$M=10$の場合の重みの値を比較してみると以下のようになる.
- $M=4~$:
array([ -0.39173338, 9.61865923, -24.48746587, 15.07254699])
- $M=10$:
array([-2.13642415e-01, 1.18629138e+02, -2.32840696e+03, 2.03425265e+04,
-9.68996625e+04, 2.71673994e+05, -4.59441029e+05, 4.59632301e+05,
-2.49977441e+05, 5.68794097e+04])
$M=10$のときの重みの値が$M=4$と比べてかなり大きいことが分かる.そのため,微小摂動に対する変化量が多くなり,モデル自体のノイズや未知データに対するロバスト性,汎化性がともに悪くなるといえる. そこで,先ほどの二乗和誤差に対し,重みに応じて誤差を足す罰則項*3を課す.このようにして,モデルの過学習を防ぐ方法を正則化(regularization)という.
$$ E({\bf w})=\frac{1}{2}||\Phi{\bf w}-{\bf t}||_{2}^{2}+\frac{\lambda}{2}||{\bf w}||_2^{2} $$
ただし,$\lambda$は設計者が任意に設定するパラメータで二乗和誤差と正則化誤差の相対的な重要度を表す.
これの微分も簡単にでき,最適値は
$$ {\bf w}^{*}=(\Phi^{T}\Phi+\lambda I)^{-1}\Phi^{T}{\bf t} $$
となる.
改めてこれを考慮し実装しなおす.
class SimpleMSE(): def __init__(self,X_train, t_train): self.X_in = X_train self.t = t_train def fit(self, M=4,l2_penalty=0 ,ndiv = 500): self.M = M phi = np.empty((self.X_in.shape[0],self.M)) for i, col in enumerate(phi.T): phi[:,i] = self.X_in**i #### 変更箇所 theta = np.linalg.solve(phi.T.dot(phi)+l2_penalty*np.eye(self.M), phi.T.dot(self.t)) #### func = lambda x: sum([th * x**i for i, th in zip(range(self.M), theta)]) return theta, func
このようにして$M=10,\lambda=10^{-4}$として実行すると以下のようになる.

うまく正則化が働いて元の曲線にかなり近似できていることが見て取れる.
$\lambda$を変えた際の曲線の変化の様子を動画にした.
うまく値を適合させるためには適切な値を与えてやる必要があることが分かる.
ここで値の適応具合を定量的に評価するため,平均二乗平方根誤差
$$E_{R M S}=\sqrt{\frac{2E({\bf w}^{*})}{N}}$$
を導入する.
$N$で割ることで,サイズの異なるデータを比較でき,平方根を取ることで目的変数と同じ単位での評価が可能となる.
def calc_mse_rmse(func, X_train, t_train): t_pred = np.array([func(x) for x in X_train]) mse = 0.5*np.sum(np.square(t_pred - t_train)) rmse = np.sqrt(2*mse/X_train.shape[0]) return mse, rmse mse = SimpleMSE(X_train, t_train) rmse1 = [] rmse2 = [] i = 0 lms = np.logspace(-20, 1, 100) for lm in lms: i += 1 theta, func = mse.fit(10, lm) display_data([lambda x:np.sin(2*np.pi * x), func], X_train, t_train, name="./imgs/{:03d}".format(i), title="$M = 9,\lambda = {:.3e}$".format(lm)) _, rmse_train = calc_mse_rmse(func, X_train, t_train) _, rmse_test = calc_mse_rmse(func, X_test, t_test) rmse1.append(rmse_train) rmse2.append(rmse_test) fig = plt.figure(figsize=(7,5)) plt.plot(lms, rmse1, label="Train_data") plt.plot(lms, rmse2, label="Test_data") plt.legend() plt.xscale('log') plt.xlabel('$\lambda$') plt.ylabel('$E_{RMS}$') plt.ylim((-0.05,1.05)) plt.show()
前半部分は動画を作るためのフレームの保存で,後半はRMS誤差のプロットである.
$\lambda$を$10^{-20}$から,$10^{1}$へ変化させていった際,RMS誤差は以下のような結果となった.

動画と比較して分かるように,元の曲線に近づくにしたがって,RMS誤差が減少していくのが分かる.
次はベイズ曲線フィッティングを実装したい.