精読 #1 An Introduction to Image Synthesis with Generative Adversarial Nets
https://arxiv.org/abs/1803.04469
要旨
GANはここ数年CVやNLP分野で劇的な進化を遂げている.特に画像合成は最も研究されている分野の一つである. この論文では,画像合成に使われる手法の分類,GANと異なるtext2imageやimage2imageのモデルとの比較,及びGANを用いた画像合成における評価指標と将来の研究の方向性について議論する.
導入
- GANの良いチュートリアル:https://arxiv.org/pdf/1701.00160.pdf
- この論文では画像合成についてのGANについて議論するが他の分野については以下の論文を参照:
- 欠落画像の補完
- 画像のキャプションの生成
- 物体検出
- セマンティックセグメンテーション
- テキスト生成
- https://arxiv.org/abs/1705.10929
- https://arxiv.org/abs/1709.08624
- 対話生成
- Q&A
- 機械翻訳
- GANをNLPのタスクで使うのは難しく,テクニックを要する https://arxiv.org/abs/1609.05473
GANの基礎
- 生成器モデル $G$
GANの生成器はノイズ$\textbf{z}$を入力とし,$G(\textbf{z};\theta)$を出力とする.出力の分布$p_g$を訓練画像の分布 $p_{data}$ を推定すべく,パラメータ $\theta$を学習する.
- 弁別器モデル$D$
訓練画像,もしくは生成された画像を入力とし,その画像が訓練画像か生成された画像かを見分けるように学習を行う.
初期のGANは全結合層を使用し,モデルを形成していたが,後のDCGANではCNNを使用することでより良いパフォーマンスを得た.
GANはよく生成器と弁別器のいたちごっこに擬えられる. すなわち,生成器が弁別器を欺くようなリアルなデータを生成し,弁別器は真偽をよりよい精度で見分けられるように双方学習を行い,高精度の画像を生成するように学習していく.
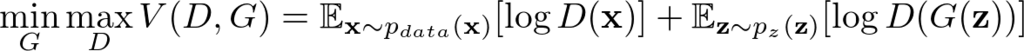
しかしながら,弁別器が生成器より学習が進んでしまうと弁別器は生成器からのサンプルを無視し,$\log{(1-D(G(\textbf{z})))}$の誤差が飽和し,生成器は勾配が0に近くなるため,何も学べなくなる. このことを防ぐため,生成器の学習の際,$\log{(1-D(G(\textbf{z})))}$を最小化するのではなく,$\log{D(G(\textbf{z}))}$を最大化する様にする.
Conditional GAN
従来のGANでは,生成される画像の種類は,入力ノイズ$\textbf{z}$にのみ依存し明示的にコントロールすることはできない. https://arxiv.org/abs/1411.1784 そこで条件付きの入力$\textbf{c}$を追加した生成器$G(\textbf c,\textbf z)$を用いて画像の生成を行う. $\textbf c$は通常,$\textbf z$に連結されて通常のGANのように生成される.また,$\textbf{c~z}$でデータオーギュメンテーションを行える.
https://arxiv.org/abs/1612.03242 $\textbf c$の目的としてはその任意性を利用して画像ならば物体の特性やテキストの説明を挿入するなどを行い生成したい画像を生成できるように誘導することを意図とする.
GAN with Auxiliary Classifier
副次的情報をより多く得るように,また,半教師あり学習を行えるようにするために追加のタスクに固有の弁別器の補助分類器を追加する.
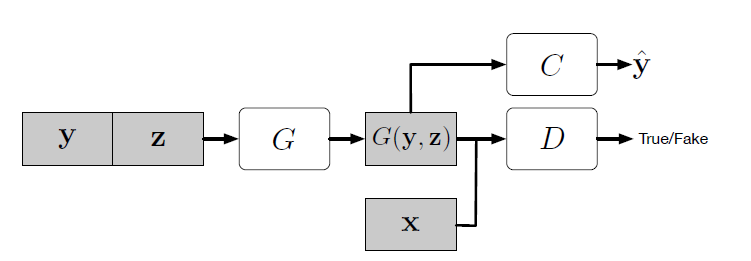
上図の$C$が補助分類器にあたり,補助分類器を追加することで,事前学習済みのモデルを使用することが可能になる. https://arxiv.org/abs/1610.09585 上記の論文でAC-GANによる画像生成は鮮明な画像を作ることを可能にしたことのほかにGANの問題の一つであるMode Collapse問題を軽減できるということが立証されている.また,このモデルは画像合成においても有用的でもある.
GAN with Encoder
従来のGANはノイズ符号$\textbf z$から合成画像$G(\textbf z)$への変換は可能であるが,その逆操作は行うことができない.ノイズ分布がデータサンプルの潜在因子空間として振舞うとしたら,GANはデータから潜在因子への写像入力能力を欠如しているといえる.
BiGAN: https://arxiv.org/abs/1605.09782
ALI: https://arxiv.org/abs/1606.00704
上記の2つの論文にて提案されている手法として,従来のGANの型に新たにエンコーダ$E$を追加するものがある.
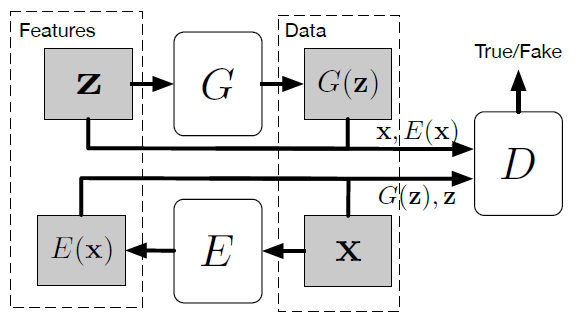
上図において弁別器$D$はノイズから生成された画像と実在の画像のほか,潜在因子ベクトルも受け取るように修正する.誤差関数は以下のように定義される.
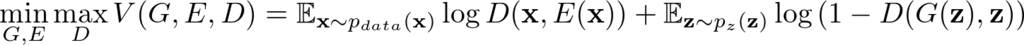
GAN with Variational Auto-Encoder
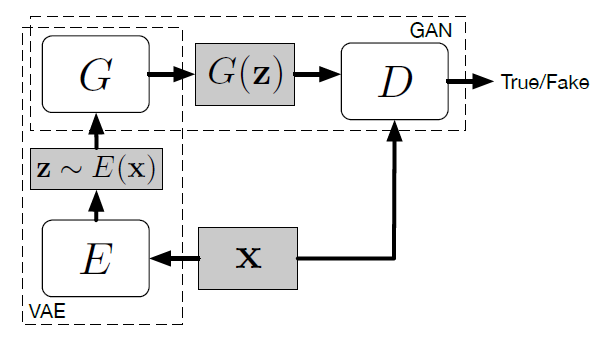
https://arxiv.org/abs/1512.09300?context=cs
VAE-GANは変分オートエンコーダとGANの双方の良い特徴をいいとこどりすることが目的である.GANはシャープな画像を生成できるがMode Collapse等の問題があり,VAEはブラーのかかった画像だが多様な画像を生成することできる.VAE部分は標準正規事前分布を科すことでエンコーダ$E$を正規化する. VAEの損失は以下のように定義される
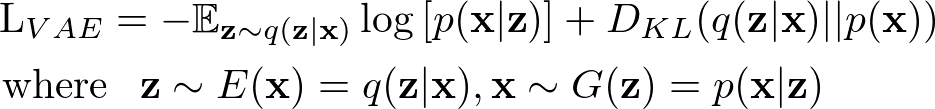
さらに,VAE-GANは弁別器$D$に関してVAEの再構成損失を表すことを提案している. $D_l(\textbf x)$を$l$番目の層の表現とすると,ガウス観測モデルは以下のように定義される.
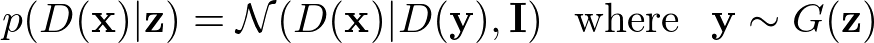
これを用いると,VAEの誤差は以下のように表すこともできる.
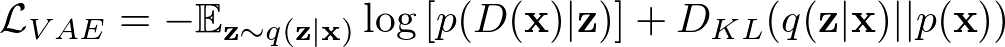
GANの誤差は従来のGANと同じものを採用している. 実験の結果,VAE-GANは単体のVAE,GANより,良い画像を生成されることが立証されている.
Mode Collapseの対処方法
GANは画像合成に非常に効果的だが,訓練過程は非常に不安定で,良い結果を得るためには多くのコツを要領よく用いる必要がある.
https://arxiv.org/abs/1406.2661
https://arxiv.org/abs/1511.06434
https://arxiv.org/abs/1506.05751
GANはさらに上記の論文で議論されている通り,Mode Collapse(モード崩壊)問題を抱えている.
従来のGANの方法では,弁別器はさまざまな種類のサンプルを考慮せずに,ただ,入力サンプルが本物か否かのみを出力する.そのため生成器が弁別器をうまくだます少量のサンプルを生成するためだけに学習を費やす危険性がある.
MNISTの例で言うなれば,0-9の画像が含まれているのにもかかわらず,極端な場合にはうち1つの数字のみを完璧に欺くように学習し,他の9つの数字を学習しないようになってしまう.これはクラス間モード崩壊の一例である.対して,ある数字の筆記方法の差異から生じるモード崩壊は内クラスモード崩壊と言われている.
https://arxiv.org/abs/1606.03498
モード崩壊を防ぐためのアプローチは多数挙げられている.そのうちの1つとして,ミニバッチ特徴量(Minibatch Features)と呼ばれるものがある.そのアイデアは弁別器に本物の画像のミニバッチと生成された画像のミニバッチとを比較させるというアイデアである.この方法を採用すると,弁別器は生成画像が他の生成画像と比較して,潜在因子空間的に近傍に位置しているかどうかを学習することができる.
https://arxiv.org/abs/1701.00160[再掲]
しかしながら,この操作がうまくいくかどうかは,距離計測のために使用する特徴量に大きく依存しているといわれている. MRGAN,BiGANではデータ空間を潜在因子空間へ射影するエンコーダを導入してこの問題の解決を試みている.エンコーダと生成器の組み合わせはオートエンコーダのように振舞い,再構成誤差がモード正則化として,敵対的損失に加算される.すなわち,弁別器は再構成されたサンプルを識別するように訓練され,また別のモード正則化器として機能するようになる.
https://arxiv.org/abs/1701.07875
WGAN(Wasserstein GAN)はWasserstein距離を実データ分布と学習データ分布間の類似性を測る測度として使用する.(従来のGANではJensen-Shannonダイバージェンスを使っている)この方法は理論的には,収束時間が従来のGANと比較して長くなっている.
https://arxiv.org/abs/1704.00028
上記の問題を軽減するために提案された手法がWGAN-GPである.この方法ではWGANで行っていたウェイトクリッピングによる制約の代わりに勾配に応じたペナルティ項を使用している.WGAN-GPは良い画像を生成し,モード崩壊をうまく回避しておりさらに,他のGANのフレームワークに足すことが容易な方法である.
GANによる画像合成の一般的アプローチ
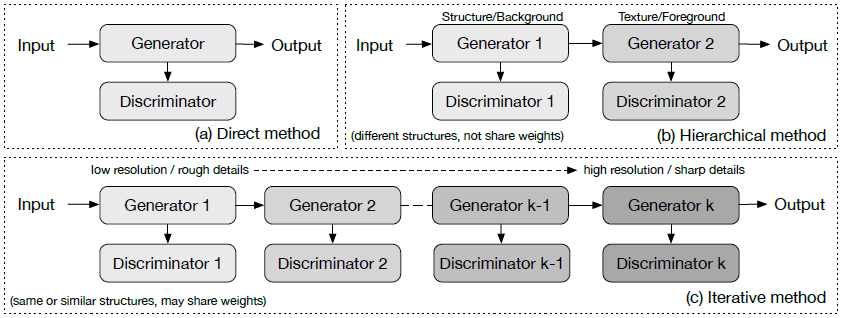
ここでは,画像生成のためのアプローチに応じて,画像生成におけるGANを次の3つの種類に分類する.
- 直接法(Direct Method)
- 階層法(Hierarchical Method)
- 反復法(Iterative Method)
直接法
1つの生成器と1つの弁別器のみを使用するモデル.どちらも,枝分かれも双方向性もない構造であり,初期のモデルの多くがこれに該当する.
- GAN
- DCGAN
- ImprovedGAN
- InfoGAN
- f-GAN
- GAN-INT-CLS
階層法
2つの生成器と2つの弁別器を使用するモデル.2つに隔てる目的としては,画像生成過程を「スタイルと構造」や「前景と背景」といった2つの構造に分け隔てることである.
https://arxiv.org/abs/1603.05631
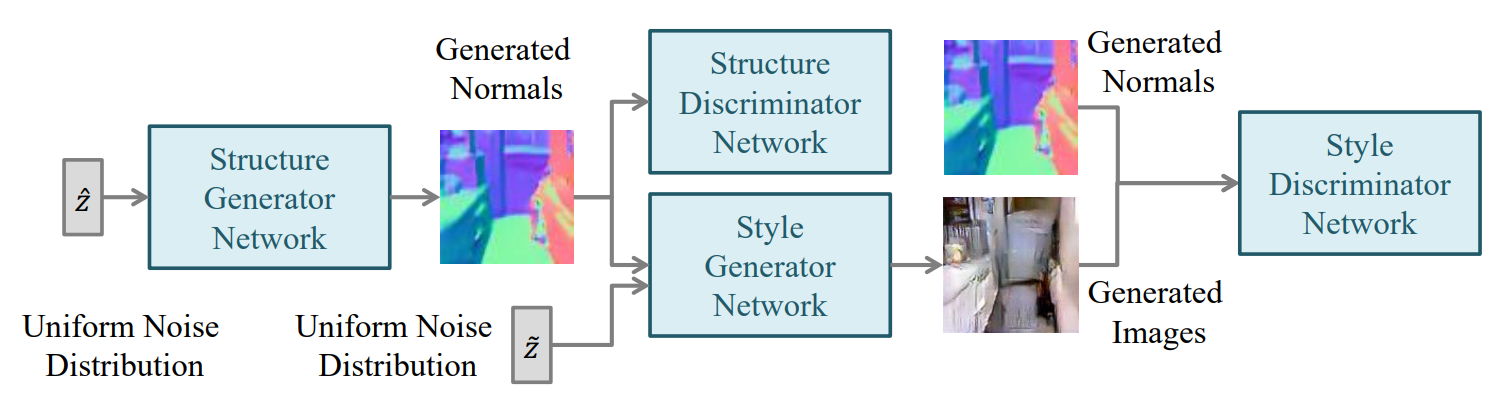
SS-GANは2つのGANを使用するモデルの一例である. まず,Structure生成器にてランダムノイズ$\hat{\textbf z}$を入力として,法線マップを生成する.生成された法線マップはStructure弁別器で真偽を判別する.Style生成器には法線画像とまた,ランダムノイズ$\textbf z$を入力とし,RGBの画像を出力する.最後に,Style弁別器にて,ノーマルマップと生成画像を入力とし,また,真偽を判別する.Structure生成器は,DCGANと同様な構造をしているが,Style生成器は少し異なっている.
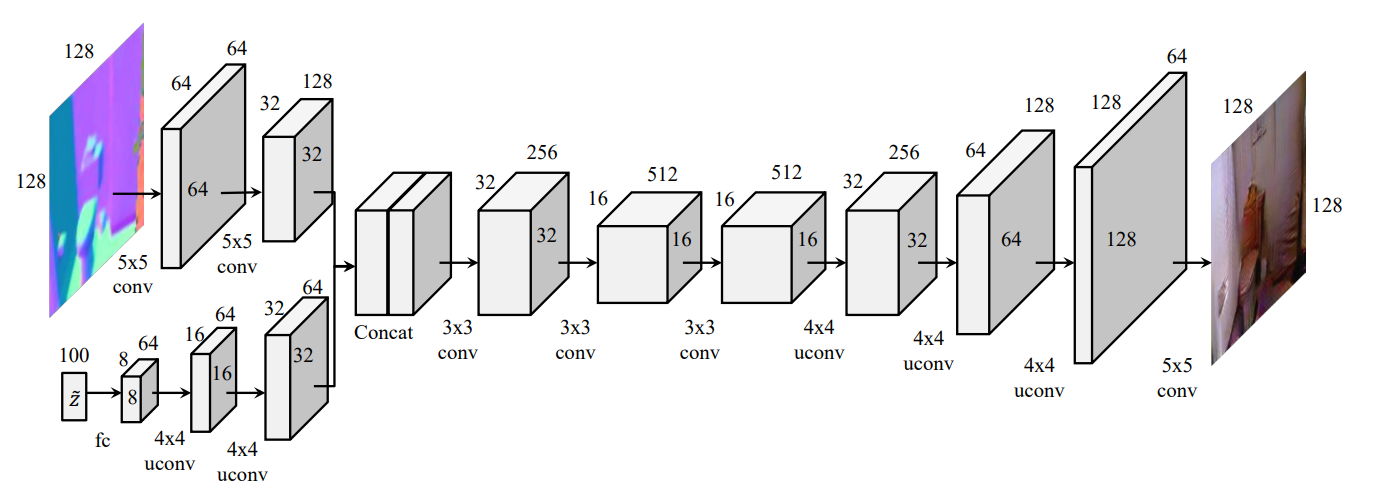
法線画像を何度か畳み込みレイヤに通し,また,ノイズを逆畳み込み層に通すなどを行い同一の縦横の長さにし2つのレイヤをチャンネル次元で連結させる.その画像をまた畳み込み層に通して,画像を新たに生成する. Style弁別器では,法線画像とそれに対応する画像をチャンネル次元で結合した画像を単一の入力として扱う.SS-GANは良質な画像を再構成するためには,良質な法線マップ情報が必要だろうという仮定の下,画像を法線マップへと射影させ,ピクセルごとに強制的に再構成法線情報を実際の画像を推定するためにピクセル単位の誤差を計算する. SS-GANの主な制約としては,画像の本当の法線情報を得るために,Kinectを使用する必要があるということである.
反復法
この方法と階層法との主な違いは,構造の似通った,もしくは全く同じな生成器をより鮮明な画像を生成するためにいくつも使用することに加え,生成器間にて重みの共有を行うという点である.
LAPGAN
https://arxiv.org/abs/1506.05751
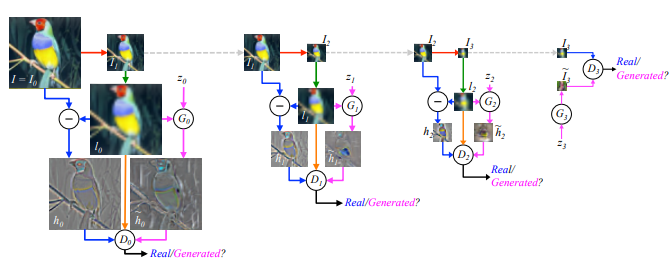
(1) $I_0$(オリジナルイメージ)を半分の大きさにダウンサンプリングし,$I_1$をつくる(赤線). (2)$I_1$を2倍でアップサンプリングし,$l_0$をつくる(緑線). (3)等確率で青線もしくはピンク線の処理を行う. (4)-A 青線の場合は$h_0=I_0-l_0$でハイパスを計算し,$D_0$は$h_0$と$l_0$を受け取り真偽を評価する (4)-B ピンク線の場合は$G_0$が$l_0$とノイズ$z_0$を受け取り,ハイパス画像を生成する.(4)-A同様$D_0$にて真偽を評価する (5)再帰的に(1)-(4)を繰り返していきある程度の大きさになったら通常のGANと同様の構造で画像生成を行う. (原著論文より訳して引用)
LAPGANは反復的な方法を始めて用いたGANのモデルである.LAPGANでは,ラプラシアンピラミッドを利用することで,鮮明な画像を生成しようと試みている. LAPGAN内の生成器はすべて前の生成器から生成されたデータとノイズを入力とし,ラプラシアンフィルタを施した画像の生成を行う.
StackGAN
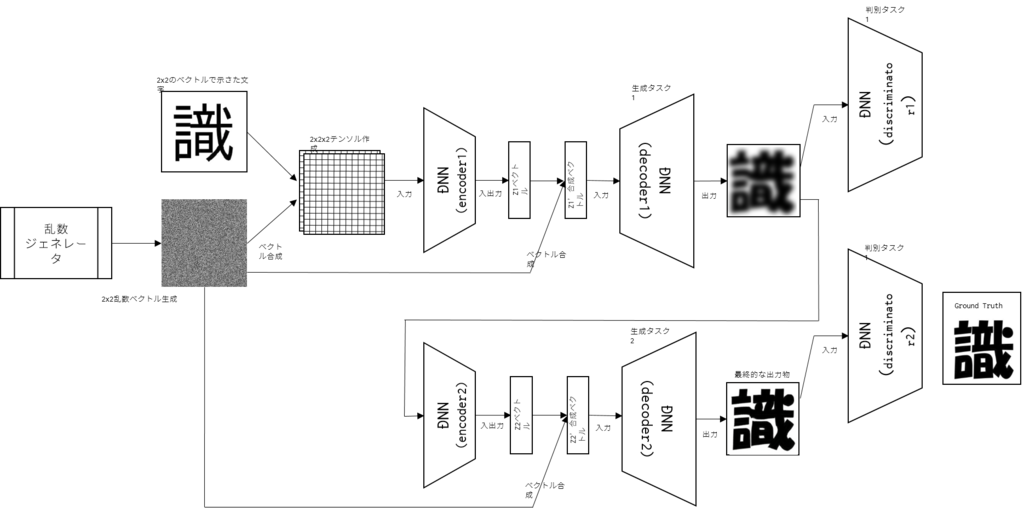
https://arxiv.org/abs/1612.03242
StackGANは反復法の一つだが生成器は2つしか存在しない. 1つ目の生成器にて$(\textbf z,\textbf c)$を受け取り,ブラーのかかった荒い画像を生成する. 2つ目の生成器では$(\textbf z,\textbf c)$と1つ目の生成器で作られた画像を入力として,より鮮明な画像を生成する.
SGAN
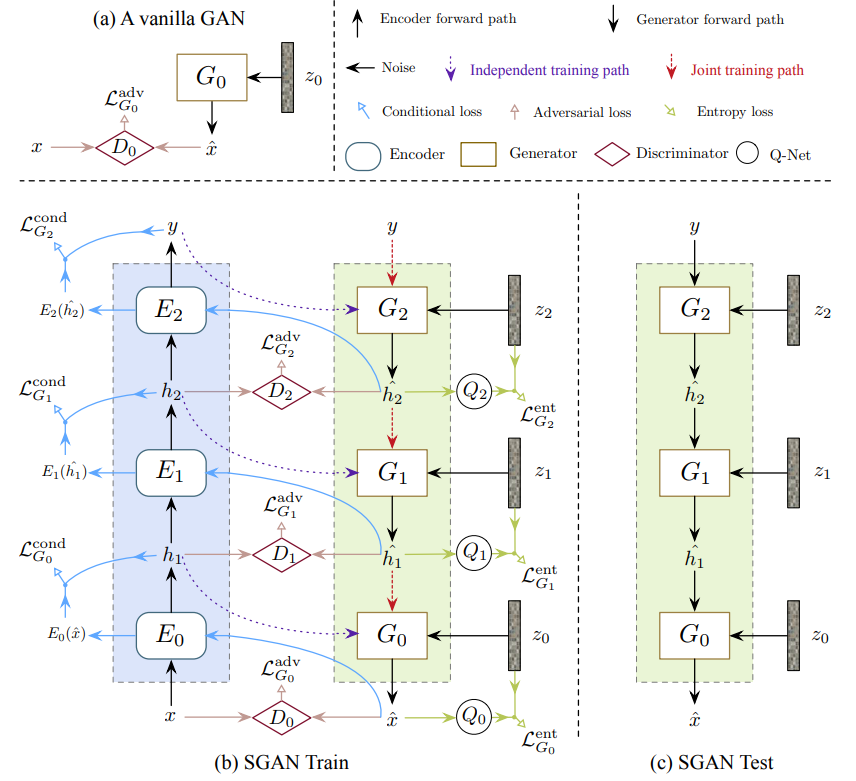
https://arxiv.org/abs/1612.04357
SGANは生成器を幾重にも積み,低レベルの潜在因子空間をより高レベルの潜在因子空間へと写像することを繰り返して鮮明な画像を生成する. さまざまな特徴量空間に別々の生成器を使用する意図としては,SGANがエンコーダ,弁別器,およびQ-ネットワーク(エントロピー最大化を行うための事後確率$P(\textbf z_i|\textbf h_i)$予測のために使用されるもの)を各生成器に関連付けして,それらの機能改善を図るためである.
その他
Progressive GAN
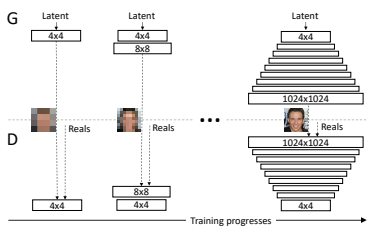
https://arxiv.org/abs/1710.10196
Progressive GANでは,はじめ$4\times4$で生成と弁別を行い,学習を行った後,倍解像度の画像を生成させる層を追加し,再度学習を行う.この操作を繰り返し,$1024\times 1024$の画像においてもかなり鮮明に画像を生成することができる.