初心に帰って変分ベイズ(2)::9/17
fgjiutx.hatenablog.com この記事の続きです
4.2. 変分事後分布の算出
モデルを変分ベイズ法で扱うために,まず,全確率変数の同時分布を求めます. $$ p({\bf X},{\bf Z},{\bf \boldsymbol\pi},{\bf\boldsymbol \mu},{\bf \Lambda})= p({\bf X}|{\bf Z},{\bf \boldsymbol\mu},{\bf \Lambda})p({\bf Z}|{\bf \boldsymbol\pi})p({\bf\boldsymbol \pi}) p({\bf\boldsymbol \mu}|{\bf \Lambda})p({\bf \Lambda}) $$ 観測変数は${\bf X}$のみであるので,変分近似は,潜在変数とパラメータに分解して,以下のように考えられます. $$ q({\bf Z},{\bf\boldsymbol \pi},{\bf \boldsymbol\mu},{\bf \Lambda})= q({\bf Z})q({\bf \boldsymbol\pi},{\bf \boldsymbol\mu},{\bf \Lambda}) $$ 前述のように,因子$q({\bf Z})$は,他方の因子の期待値を求めることで,最適化でき, $$ \ln q^{\star}({\bf Z})=\mathbb E_{\pi,\mu,{\bf \Lambda}} [\ln p({\bf X},{\bf Z},{\bf \boldsymbol\pi},\boldsymbol\mu,{\bf \Lambda})]+\text{const} $$ 同次分布の分解式から,${\bf Z}$にかかわる項だけを抜き出すことで,以下のように式変形をすることができます. $$ \ln q^{\star}({\bf Z})=\mathbb E_{\boldsymbol\pi,\boldsymbol\mu,{\bf \Lambda}} [\ln p({\bf Z}|\boldsymbol\pi)]+ \mathbb E_{\boldsymbol\pi,\boldsymbol\mu,{\bf \Lambda}} [\ln p({\bf X}|{\bf Z},\boldsymbol\mu,{\bf \Lambda})]+\text{const} $$ ここに,実際の式を代入することで, $$ \ln q^{\star}({\bf Z})=\sum_{n=1}^{N}\sum_{k=1}^{K}z_{nk}\ln \rho_{nk} + \text{const} $$ となります.ただし, $$ \ln\rho_{nk}=\mathbb E[\ln \pi_k]+\frac{1}{2}\mathbb E[\ln {\bf |\Lambda_k|}] -\frac{D}{2}\ln 2\pi-\frac{1}{2}\mathbb E_{\boldsymbol\mu_k,{\bf \Lambda}_k} [({\bf x}_n-\boldsymbol\mu_k)^{T}{\bf \Lambda}_k({\bf x}_n-\boldsymbol\mu_k)] $$ で,$D$はデータの次元です.
式の指数を取ると, $$ q^{\star}({\bf Z})\propto\prod_{n=1}^{N}\prod_{k=1}^{K}\rho_{nk}^{z_{nk}} $$ となり,この分布は正規化されている必要があるので, $$ r_{nk}:=\frac{\rho_{nk}}{\displaystyle \sum_{j=1}^{K}\rho_{nj}} $$ とすることで, $$ q^{\star}({\bf Z})=\prod_{n=1}^{N}\prod_{k=1}^{K}r_{nk}^{z_{nk}} $$ が,得られます.この最適化の式は,式中に他のパラメータが出てきているため,相互依存関係にあり双方を繰り返し更新していく必要があります.
次に,$q^{\star}({\bf \pi},{\bf \mu},{\bf \Lambda})$を考えます.
$q^{\star}({\bf Z})$と同様,一般的な変分推定の式$\ln q^{\star}(\boldsymbol\pi,\boldsymbol\mu,{\bf \Lambda})=\mathbb E_{{\bf Z}}[\ln p({\bf X},{\bf Z},{\bf \boldsymbol\pi},\boldsymbol\mu,{\bf \Lambda})]+\text{const}$から, $$ \ln q({\bf \boldsymbol\pi},{\bf \boldsymbol\mu},{\bf \Lambda})= \ln p(\boldsymbol\pi)+\sum_{k=1}^{K}\ln p(\boldsymbol\mu_k,{\bf \Lambda}_k)+\mathbb E_{{\bf Z}} [\ln p({\bf Z}|\boldsymbol\pi)]+\sum_{k=1}^{K}\sum_{n=1}^{N}\mathbb E[z_{nk}] \ln \mathcal N({\bf x}_n|\mu_k,{\bf \Lambda}_k^{-1})+\text{const} $$ と分解されます.
分解された式は,$\pi$を含む項と,$\boldsymbol\mu,{\bf \Lambda}$を含む項に分割することができるので,$q({\bf \boldsymbol\pi},{\bf \boldsymbol\mu},{\bf \Lambda})$は, $$ q({\bf \boldsymbol\pi},{\bf \boldsymbol\mu},{\bf \Lambda})=q(\boldsymbol\pi)\prod_{k=1}^{K}q(\boldsymbol\mu_k,{\bf \Lambda}_k) $$ となり,$q^{\star}(\pi)$は $$ \ln q^{\star}(\boldsymbol\pi)=\ln p(\boldsymbol\pi)+\mathbb E_{\bf Z}[\ln p({\bf Z}|\boldsymbol\pi)]+\text{const} $$ から,$p({\bf \pi})$は, $$ \begin{eqnarray} \ln p({\bf \boldsymbol\pi})&=& \ln \left(C(\alpha_0)\prod_{k=1}^{K}\pi_{k}^{\alpha_{0}-1}\right)\\ &=&(\alpha_0-1)\sum_{k=1}^{K}\ln \pi_k+\text{const} \end{eqnarray} $$ となって,$\mathbb E_{\bf Z}[\ln p({\bf Z}|\boldsymbol\pi)]$は $$ \begin{eqnarray} \mathbb E_{\bf Z}[\ln p({\bf Z}|\boldsymbol\pi)]&=&\mathbb E_{{\bf Z}} \left[\ln\left(\prod_{n=1}^{N}\prod_{k=1}^{N}\pi_{k}^{z_{nk}}\right)\right]\\ &=&\sum_{k=1}^{N}\sum_{k=1}^{N}\mathbb E_{{\bf Z}}[z_{nk}]\ln \pi_k+\text{const} \end{eqnarray} $$ $z_{nk}$は0もしくは1をとるので期待値は容易に計算でき,$\mathbb E_{\bf Z}[z_{nk}]=r_{nk}$となるので, $$ \mathbb E_{\bf Z}[\ln p({\bf Z}|\boldsymbol\pi)]=\sum_{k=1}^{N}\sum_{k=1}^{N}r_{nk}\ln \pi_k+\text{const} $$ となるので,結局, $$ \ln q^{\star}(\boldsymbol\pi)=(\alpha_0-1)\sum_{k=1}^{K}\ln \pi_k+\sum_{k=1}^{N}\sum_{k=1}^{N}r_{nk}\ln \pi_k+\text{const} $$ となります.ここで,指数を取ると, $$ q^{\star}(\pi)=\prod_{k=1}^{K}\pi_{k}^{\alpha_0+\sum_{n=1}^{n}r_{nk}-1} $$ より,$N_k=\sum_{n=1}^{n}r_{nk}$,${\bf \alpha}_k=\alpha_0+N_k$とすると,$q^{\star}(\pi)$はディリクレ分布に従うことが分かります. $$ \ln q^{\star}(\boldsymbol\pi)=\text{Dir}(\boldsymbol\pi|\boldsymbol \alpha) $$ つぎに,$q(\boldsymbol\mu_k,{\bf \Lambda}_k)$は,乗法定理から$q^{\star}(\boldsymbol \mu_k,\boldsymbol \Lambda_k)=q^{\star}(\boldsymbol\mu_k|\boldsymbol\Lambda_k)q^{\star}(\boldsymbol\Lambda_k)$となるので,変分推定式から$\boldsymbol \mu_k,\boldsymbol \Lambda_k$の項を抜き出して(長い)式変形をすると,ガウス-ウィシャート分布となることが分かります.
ここで,ガウス-ウィシャート分布を考えるうえで次のコンポーネント(クラスタ)ごとの加重平均した統計量を用いると式の簡便化が見込めます. $$ \begin{eqnarray} \bar{{\bf x}_k}&=&\frac{1}{N_k}\sum_{n=1}^{N}r_{nk}{\bf x}_n\\ {\bf S}_k&=&\frac{1}{N_k}\sum_{n=1}^{N}r_{nk}({\bf x}_n-\bar{\bf x}_k) ({\bf x}_n-\bar{\bf x}_k)^{T} \end{eqnarray} $$ この補助的な統計量を用いると, $$ q^{\star}(\boldsymbol\mu_k,\boldsymbol\Lambda_k)=\mathcal N(\boldsymbol\mu_k|{\bf m}_k,(\beta_k\boldsymbol\Lambda_k)^{-1}) \mathcal W(\boldsymbol\Lambda_k|{\bf W}_k,\nu_k) $$ と表されます.ただし, $$ \begin{eqnarray} \beta_k&=&\beta_0+N_k\\ {\bf m}_k&=&\frac{1}{\beta_k}(\beta_0{\bf m}_0+N_k\bar{\bf x}_k)\\ {\bf W}^{-1}&=&{\bf W}_0^{-1}+N_k{\bf S}_k+\frac{\beta_0N_k}{\beta_0+N_k} (\bar{\bf x}_k-{\bf m}_0)(\bar{\bf x}_k-{\bf m}_0)^{T}\\ \nu_k&=&\nu_0+N_k \end{eqnarray} $$ とします.
これらを振り返ると,
- モデルの現在の事後分布から負荷率に当たる$r_{nk}$を計算する
- その計算された負荷率をもとに事後分布を更新する
という,最尤推定におけるEMアルゴリズムに似た方法で,最適化を行えばよいということがわかります.また,$r(\propto \rho)$を計算するにあたり,パラメータの分布の期待値が必要となるがこれらは容易に計算することができて, $$ \begin{eqnarray} \mathbb E_{\boldsymbol\mu_k,{\bf \Lambda}_k} [({\bf x}_n-\boldsymbol\mu_k)^{T}{\bf \Lambda}_k({\bf x}_n-\boldsymbol\mu_k)] &=&D\beta_k^{-1}+\nu_k(\bar{\bf x}_k-{\bf m}_0)^{T}{\bf W}_k (\bar{\bf x}_k-{\bf m}_0)\\ \ln\tilde\Lambda_k:=\mathbb E[\ln|\boldsymbol\Lambda_k|]&=&\sum_{i=1}^{D} \psi\left(\frac{\nu_k+1-i}{2}\right)+D\ln2+\ln|{\bf W}_k|\\ \ln\tilde\pi_k:=\mathbb E[\ln \pi_k]&=&\psi(\alpha_k)-\psi(\hat\alpha),~ \text{where}~\hat\alpha=\sum_{k=1}^{K}\alpha_k \end{eqnarray} $$ となります.ただし,$\psi(\cdot)$はディガンマ関数と呼ばれるもので, $$ \psi(a):=\frac{d}{da}\ln\Gamma(a) $$ と定義されます.
これらの結果から, $$ r_{nk}\propto \tilde\pi_k\tilde\Lambda^{1/2}\exp\left(-\frac{D}{2\beta_k} -\frac{\nu_k}{2}({\bf x}_n-{\bf m}_k){\bf W}_k({\bf x}_n-{\bf m}_k)^{T}\right) $$ となります.
これにより,更新を繰り返してモデルを最適化する準備ができました.
4.3. 予測分布の計算
モデルに対してパラメータを最適化させた後は,未知の観測値に対して,予測分布を算出することが目的である場合がおおいので,新たな観測値$\hat x$に対して,分布$p(\hat x|{\bf X})$を求めることを考えます.
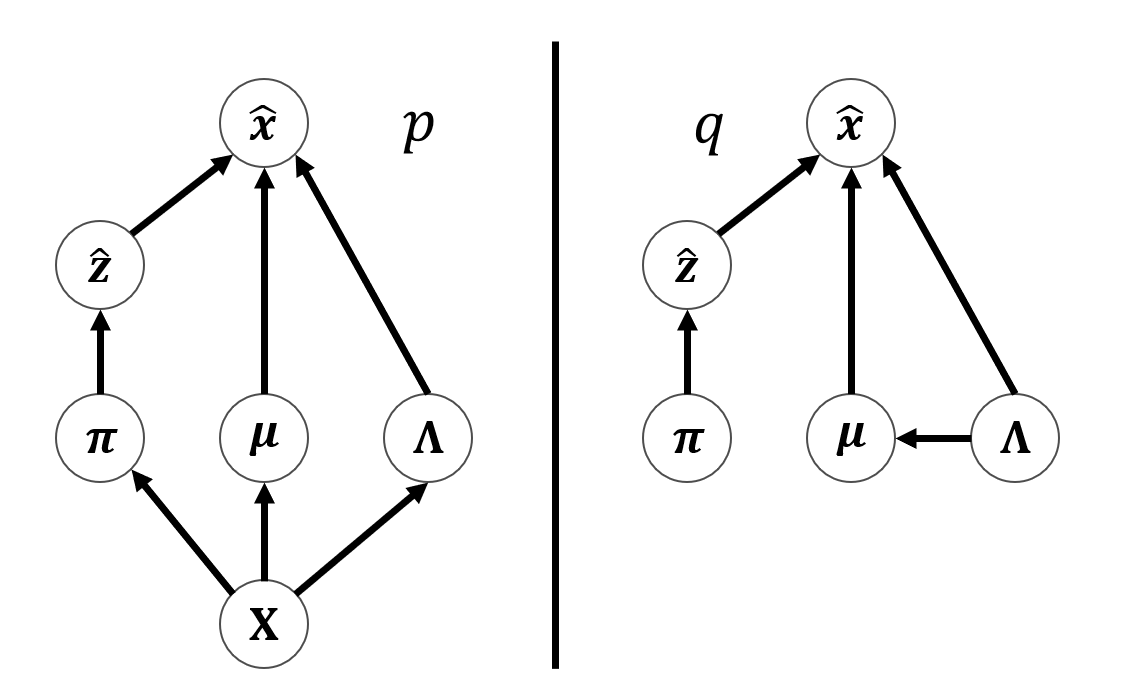
上図のようなグラフィカルモデルより考えると,分布の式が分かりやすくなり, $$ p(\hat x|{\bf X})=\sum_{\hat{\bf z}}\iiint p(\hat{\bf x}|\hat{\bf z},\boldsymbol\mu,\boldsymbol\Lambda) p(\hat{\bf z}|\boldsymbol\pi)p(\boldsymbol\pi,\boldsymbol\mu,\boldsymbol\Lambda|{\bf X})\text{d}\boldsymbol\pi \text{d}\boldsymbol\mu\text{d}\boldsymbol\Lambda $$ のように周辺化を行うことで達成されます.
いま,変分近似を用いて実パラメータ分布を$p(\boldsymbol\pi,\boldsymbol\mu,\boldsymbol\Lambda|{\bf X})\approx q(\boldsymbol\pi)q(\boldsymbol\mu,\boldsymbol\Lambda)$と近似したので, $$ \begin{eqnarray} p(\hat{\bf z}|{\bf \boldsymbol\pi})&=&\prod_{k=1}^{K}\pi_k^{\hat z_k}\\ p(\hat{\bf x}|\hat{\bf z},{\bf \boldsymbol\mu},{\bf \Lambda})&=&\prod_{k=1}^{K}\mathcal N({\bf x}_n|{\bf \boldsymbol\mu}_k,{\bf \Lambda}_k^{-1})^{\hat z_{k}}\\ \sum_{\hat{\bf z}} p(\hat{\bf z}|{\bf \boldsymbol\pi})p(\hat{\bf x}|\hat{\bf z},{\bf \boldsymbol\mu},{\bf \Lambda})&=&\sum_{k=1}^{K}\pi_k \mathcal N({\bf x}_n|{\bf \boldsymbol\mu}_k,{\bf \Lambda}_k^{-1})\\ p(\hat x|{\bf X})&\approx&\sum_{k=1}^{K}\iiint\pi_k \mathcal N({\bf x}_n|{\bf \boldsymbol\mu}_k,{\bf \Lambda}_k^{-1})q(\boldsymbol\pi)q(\boldsymbol\mu_k,\boldsymbol\Lambda_k)\text{d}\boldsymbol\pi \text{d}\boldsymbol\mu_k\text{d}\boldsymbol\Lambda_k \end{eqnarray} $$ となり,この積分は,なんとびっくり解析的に解くことができて,混合[多変量スチューデントt-分布](https://en.wikipedia.org/wiki/Multivariate_t-distribution)となります. $$ p(\hat x|{\bf X})\approx\frac{1}{\hat\alpha}\sum_{k=1}^{K} \text{St}(\hat{\bf x}|{\bf m}_k,{\bf L}_k,\nu_k-1+D) $$ ただし, $$ {\bf L}_k=\frac{(\nu_k+1-D)\beta_k}{1+\beta_k}{\bf W}_k $$ です.
4.4. 実装
import numpy as np from numpy.linalg import slogdet from sklearn import datasets from scipy.stats import multivariate_normal, wishart from scipy.special import gamma, digamma, loggamma import scipy.stats as stats import matplotlib.cm as cm import matplotlib.pyplot as plt from IPython.display import clear_output import os
高度な確率分布が多く出てくるため,scipyを多用します.ただし,多変量スチューデントt-分布はscipyにはないので,こちらを参照に自力で実装します.
def multivariate_student_t(x, mu, Sigma, df): x = np.atleast_2d(x) nD = Sigma.shape[0] numerator = gamma(1.0 * (nD + df) / 2.0) denominator = ( gamma(1.0 * df / 2.0) * np.power(df * np.pi, 1.0 * nD / 2.0) * np.power(np.linalg.det(Sigma), 1.0 / 2.0) * np.power( 1.0 + (1.0 / df) * np.diagonal( np.dot( np.dot(x - mu, np.linalg.inv(Sigma)), (x - mu).T) ), 1.0 * (nD + df) / 2.0 ) ) return 1.0 * numerator / denominator
さて,ここでこれから3次元テンソルの積を含むような計算を行っていくのですが,numpyで3次元以上の配列(テンソル)の積を扱いたいときに,非常に便利なものとして,numpy.einsumがあります.
その前に...
4.4.1. アインシュタインの縮約記法
たとえば,ベクトル$\boldsymbol a=(a_1,a_2),\boldsymbol b=(b_1,b_2)$の内積は, $$ \boldsymbol a\cdot\boldsymbol b=a_1b_1+a_2b_2 $$ で,一般の$n$次元ベクトルの場合には$\sum$記号を使って, $$ \boldsymbol a\cdot\boldsymbol b=\sum_{i=1}^{n}a_ib_i $$ のように表すことができます.
アインシュタインの記法は大胆にもこの$\sum$を省略して, $$ \boldsymbol a\cdot\boldsymbol b=a_ib_i $$ だとか$a_\mu b^{\mu}$のように書き表す方法です.
np.einsumはこの縮約記法を用いてテンソル積を定義するものです.
例えば,この内積は,
a = np.arange(3) # [0 1 2] b = np.arange(3) # [0 1 2] print(np.einsum("i, i ->", a, b)) # 5
と書くことができます.
第一引数がアインシュタインの縮約記法にあたり,->の左側にカンマ区切りでテンソルの縮約記法を並べ,右側に出力テンソルの記法を書きます.ただし,スカラー値の場合は省略します.
これを用いれば,様々な種類のテンソルの乗算を分かりやすく書き下すことができます.
スカラー値×ベクトル
a = 4 b = np.arange(3) print(np.einsum(", i ->i", a, b)) # [0 4 8]
2次元行列×ベクトル=ベクトル($Ax=b$)
a = np.arange(6).reshape((2, 3)) # [[0 1 2],[3 4 5]] b = np.arange(3) print(np.einsum("ij, j -> i", a, b)) # [ 5 14]
$\boldsymbol a^{T}\boldsymbol W\boldsymbol b,\boldsymbol a\in\mathbb R^{k\times j},\boldsymbol b\in\mathbb R^{k\times i},\boldsymbol W\in\mathbb R^{k\times i\times j}$
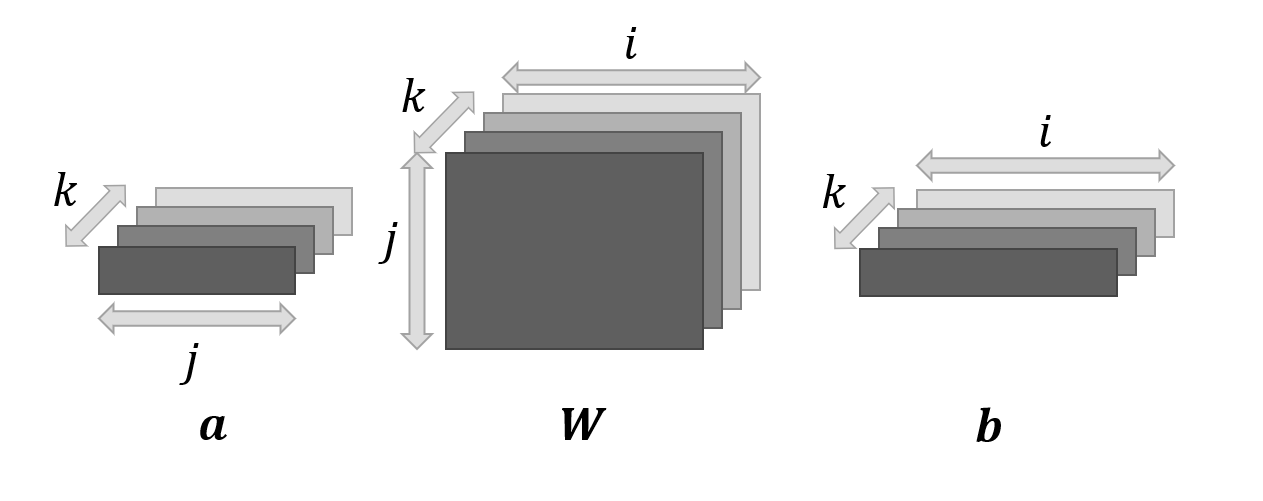
a = np.arange(6).reshape((2, 3)) W = np.arange(24).reshape((2, 4, 3)) b = np.arange(8).reshape((2, 4)) print(np.einsum("kj, kij, ki -> k", a, W, b)) # [ 156 4844]
4.4.2. クラスの実装
class VariationalMixtureGaussian(object): def __init__(self, num_clusters=3): ''' クラスの初期化 することはせいぜいクラスタ数の指定ぐらい ''' def expectation(self, X): ''' X: データ 期待値を求める過程 返り値は負荷率 r ''' def is_converged(self): ''' 収束の判定 返り値 bool値 ''' def maximization(self, X, r): ''' X: データ r: 負荷率 事後分布の最大化過程 ''' def elbo(self): ''' (未解説)変分下限を求める 返り値 スカラー値 ''' def fit_init(self, X): ''' X: データ 最適化の初期化を行う ''' def fit_1(self, X, i): ''' X: データ i: 最適化を回した回数(printの為に使用) 1回のみ最適化操作を行う ''' def fit(self, X, num_iter=1000): ''' X: データ num_iter: 最適化回数の上限 最適化操作を行う ''' def predict(self, X): ''' X: データ 新たな入力データに対する予測分布の確率を返す ''' def classify(self, X): ''' データの分類を行う 方法は 1. E過程をしてデータ点の負荷率を計算 2. argmaxを取って分類する '''
def multivariate_student_t(x, mu, Sigma, df): def __init__(self,num_clusters=3): self._param = None self.num_clusters = num_clusters def expectation(self, X): pi = digamma(self.alpha) - digamma(self.alpha.sum()) det_Wk = np.linalg.slogdet(self.W)[1] Lambda = digamma((self.nu - np.arange(2)[:,np.newaxis])/2).sum(axis=0)+\ self.ndim*np.log(2) + det_Wk pi = np.exp(pi) Lambda = np.sqrt(np.exp(Lambda)) d = X[:, :, None] - self.m.T var = np.exp( - 0.5 * self.ndim / self.beta - 0.5 * self.nu * np.einsum('nik, kij, njk -> nk', d, self.W, d) ) r = pi*Lambda*var r /= r.sum(axis=-1, keepdims=True) r[np.isnan(r)] = 1e-9 self.pi = pi self.Lambda = Lambda self.r = r return r def is_converged(self): if self._param is None: self._param = [self.m, self.W.ravel(), self.alpha, self.beta, self.nu] return False param = [self.m, self.W.ravel(), self.alpha, self.beta, self.nu] if np.array([np.allclose(self._param[i], param[i], rtol=1e-3) for i in range(len(param))]).all(): return True else: self._param = param return False def maximization(self, X, r): Nk = np.sum(r, axis=0) xk = 1/Nk * X.T.dot(r) dev = X[:,:,None] - xk Sk = 1/Nk * np.einsum("nik,njk->ijk", dev,r[:,None,:]*dev) self.beta = self.beta0 + Nk self.alpha = self.alpha0 + Nk self.m = ((self.beta0 * self.m0[:, None] + Nk * xk) / self.beta).T W0inv = np.tile(np.linalg.inv(self.W0), (self.num_clusters, 1, 1)) d = (xk - self.m0[:,None]) var = np.einsum("ik,jk->kij",d,d) bn = self.beta0*Nk/(self.beta0+Nk) self.W = W0inv + (Nk.reshape((1,1,-1))*Sk).transpose((2,0,1))+\ (bn.reshape((-1,1,1))*var) self.W = np.linalg.inv(self.W) self.nu = self.nu0 + Nk self.Sk = Sk.transpose((2,0,1)) self.xk = xk self.Nk = Nk def elbo(self): pass def fit_init(self, X): self.elbos = [] self.num_samples, self.ndim = X.shape self.m0 = np.zeros(self.ndim) self.W0 = np.eye(self.ndim) self.beta0 = 1. self.alpha0 = 1. self.nu0 = self.ndim self.m = X[np.random.choice(self.num_samples, self.num_clusters,replace=False)] self.W = np.tile(np.eye(self.ndim), (self.num_clusters, 1, 1)) self.alpha = np.ones((self.num_clusters)) self.beta = np.ones((self.num_clusters)) * self.beta0 self.nu = np.ones(self.num_clusters) * self.ndim def fit_1(self, X, i): r = self.expectation(X) self.r = r self.maximization(X, r) # self.elbos.append(self.elbo()) if self.is_converged(): print('Iter:{} all parameter converged'.format(i+1)) return True return False def fit(self, X, num_iter=1000): self.fit_init(X) for i in range(num_iter): if self.fit_1(X,i): break else: print("parameters may not be converged yet") def predict(self, X): s_alpha = self.alpha.sum() L = np.array([((self.nu + 1 -self.ndim) * self.beta / (1 + self.beta))[k] *\ self.W[k]for k in range(len(self.W))]) St =lambda k : multivariate_student_t(X,self.m[k], np.linalg.inv(L[k]), self.nu[k] + 1 - self.ndim + 1) prob = np.sum(np.array([self.alpha[k] * St(k) for k in range(len(self.W))]), axis=0)/s_alpha return prob def classify(self, X): r = self.expectation(X) return np.argmax(r, axis=1)
テンソルを扱う際のアインシュタインの縮約記法が非常に便利であることが見て取れるのではないかと思います.
実際にクラスタリングを行ってみましょう.
def plot(model, X,title='Variational Gaussian Mexture Model',ndiv=100,save=None): plt.figure(figsize=(7,7)) X0_range = X[:,0].min()-1, X[:,0].max()+1 X1_range = X[:,1].min()-1, X[:,1].max()+1 Y = model.classify(X) x, y = np.meshgrid(np.linspace(*X0_range,num=ndiv), np.linspace(*X1_range,num=ndiv)) plt.scatter(x=X[:, 0], y=X[:,1], alpha=0.6,c=cm.jet(Y / Y.max())) Z = model.predict(np.array([x.ravel(), y.ravel()]).T).reshape(x.shape) CS = plt.contour(x, y, Z, cmap='jet', alpha=0.7) plt.clabel(CS, inline=1, fontsize=10) for mu,var in zip(model.m, model.W): plt.scatter(mu[0], mu[1], marker='o', facecolors='red', edgecolors='black', s=70, alpha=0.7) plt.title(title) if save is not None: plt.savefig(save)
plt.figure(figsize=(7,7)) X, y = datasets.make_blobs(n_features=2, centers=4, n_samples=300) plt.scatter(X[:,0],X[:,1]) model = VariationalMixtureGaussian(7) model.fit(X, 10000) plot(model, X, ndiv=50)
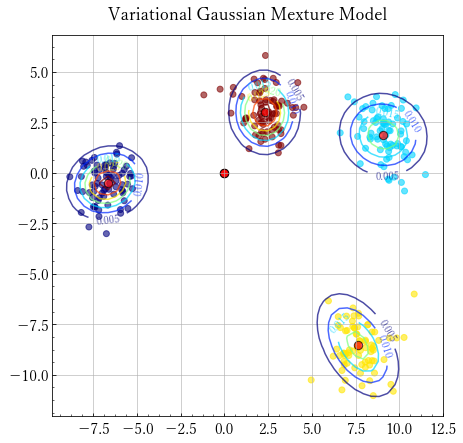
収束の様子をアニメーションにしたものは以下のようになる.
変分下界を追加した pic.twitter.com/BevHDvpLhP
— ツナ缶 (@fujifog) 2018年9月1日
コーヒーブレイク
markdownエディタとしておすすめなのがTyporaです.
いままで触ってきた中でかなり使いやすいエディタだと思います.
この記事がとても詳しく,プレビュー表示画面というものが存在しなく,表やTODOの追加などを視覚的に行えて(Dropbox Notepaperがエディタとしては近い)
CSSでスタイルを変更でき,論文チックな見やすい見た目に変更することができます.

下書きをいままでHackMDで書いていたのですが操作性可視性ともにこちらに軍配が上がっており,これからはこれをメインに使って行こうかと思います.
はかどるよ
パプリカまだみてないのでいつか見てみたい