初心に帰って変分ベイズ(1)::8/31
1. 確率モデルの近似法
確率モデルでは,観測データ${\bf X}$に対するモデルの潜在変数${\bf Z}$の事後分布$p({\bf Z}|{\bf X})$を求めることが目的です.しかしながら,「確率」として取り扱うには総和が1である(=正規化する)必要があります.ベイズの定理においては分母に相当すると言えて, $$ p({\bf Z}|{\bf X})=\frac{p({\bf X}|{\bf Z})p({\bf Z})}{p({\bf X})} $$ というベイズの式から,分母の周辺尤度$p({\bf X})$は分子を$d{\bf Z}$で積分(=周辺化)を行うことで得られて $$ p({\bf X})=\int p({\bf X}|{\bf Z}) p({\bf Z})d{\bf Z} $$ という式になります.
しかしながら,尤度関数($p({\bf X}|{\bf Z})$)事前分布($p({\bf Z})$)がどちらも正規分布などという簡単な条件下では解析的に解けるものの,複雑な一般の問題ではこの計算を行えない場合が多いです. というのも,潜在変数空間の次元数が膨大であったり,積分が閉じた形式*1の解を持たないといったことが主な理由です.
解析的に求まらない問題に対しては何を行うかと言えば,やはり近似です.
よく使われる近似法としては
- マルコフ連鎖モンテカルロ(MCMC)
- 変分ベイズ法(変分推定法)
があり,前者が確率的近似に対して後者が決定的近似です.
MCMCについての詳細は後に述べるとしてそれぞれ以下のような長所と短所が存在します.
| 長所 | 短所 | |
|---|---|---|
| MCMC | $N\rightarrow\infty$ならば厳密解が得られる | 計算量が嵩む |
| 変分ベイズ法 | 計算が少ない | 厳密解は得られない |
変分ベイズ法は複雑な事後分布を分解し近似を行うというスタンスで学習を行います.
その理論の導出の前に,導出の際に用いるKLダイバージェンスについて今だ理解が足りてなかったのでまとめます*2.
2. エントロピーとKLダイバージェンス
2.1. エントロピー
情報学における(離散分布の)エントロピーは以下のように定義でき, $$ I(X)=-\sum_{i}p(i)\log{p(i)} $$ 名の示す通り,統計力学のエントロピーと同様,確率変数$X$の取りうる「乱雑さ」を定量的に表す指標といえます.
例えば,6面体サイコロ$X=[1,2,3,4,5,6]$を考えたとき出目の確率が
- $p(X)=[1/5, 1/10, 1/10, 1/5, 1/5, 1/5]$
- $q(X)=[1/2,1/4,1/8,1/16,1/32,1/32]$
- $r(X)=[1/6,1/6,1/6,1/6,1/6,1/6]$
であるします.
エントロピーはこの場合出目が偏らないほど予測が行いづらいので,いわば出目の予測のしにくさを表す量ともいえます.
それぞれのエントロピーをpythonで求めてみます.
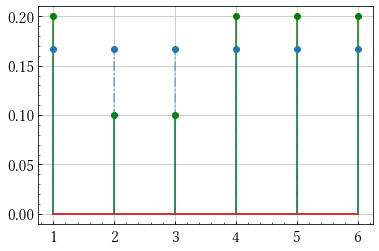
import numpy as np import matplotlib.pyplot as plt x = np.arange(1,7) q = np.array([1/2, 1/4, 1/8, 1/16, 1/32, 1/32]) p = np.array([1/5, 1/10, 1/10, 1/5, 1/5, 1/5]) r = np.ones(6)/6 # 2つの確率分布を可視化する関数です def plot(p, q): m, s, b = plt.stem(x, p) plt.setp(m, 'color', 'g') plt.setp(s, 'color', 'g') m, s, b = plt.stem(x, q) plt.setp(s, 'linestyle', '-.', 'alpha', 0.6) plt.show() # エントロピーの定義 H = lambda p: -np.sum(p*np.log(p)) print(H(p)) # 1.74806... print(H(q)) # 1.3429... print(H(r)) # 1.79175...
pとrの分布
qとrの分布
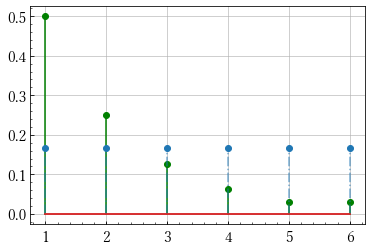
予測通り同様に確からしいサイコロのエントロピーが最も大きいことが分かりました.
また,pとrをみると定義式から見ても明らかですが似た分布ではエントロピーの値が近いことも言えます.
2.2. KLダイバージェンス
二つの確率分布$p,q$に対して距離的な解釈を与えたいとします.すなわち,本来の分布$p$から,実際の分布$q$がどの程度離れているかを考えます.
そこで,下式より定義されるKLダイバージェンスを導入します.
$$ D_{KL}(p||q)=\sum_{i}p_i\log{\frac{p_i}{q_i}} $$
これは変形すると$-p_{i}\log{q_{i}}$と$-p_{i}\log{p_{i}}$の差に分解されるので「$q$に従ってデータが発生したと想定して計算したエントロピー」と「実際に$p$に従って観測されたデータによるエントロピー」の差であると解釈できます*3.
また,定義からもわかるように可換ではありません.
サイコロの例で実際に計算してみると,
D_KL = lambda p, q:np.sum(p*np.log(p/q)) print(D_KL(p, r)) # 0.043692... print(D_KL(r, p)) # 0.048727... print(D_KL(q, r)) # 0.448786...
分布が似ている$p,r$では低い値を取ることが確認できます.
もちろん,KLダイバージェンスは総和を適切に積分に置き換えることで連続な確率変数に対しても適用することが可能です.

このグラフは$p$が標準正規分布に従い,$q(x)$を$q(x)\sim\mathcal N(x;\mu_{q},\sigma_{q})$として横軸を$\mu_{q}$,縦軸を$\sigma_{q}$としたときのKLダイバージェンスをカラーマップで表したものです.$\mu_{q}=0,\sigma_{q}=1$の際に最も青く表示されていることが見て取れます.
定義からもわかるようにKLダイバージェンスは非負で0となるのは分布が完全に等しいときのみという性質があります.
3. 変分ベイズ
3.1. 変分下界
KLダイバージェンスが分布の類似度を測るものだということが分かりました.なので,確率モデルの事後分布$p({\bf Z}|{\bf X})$を分布$q({\bf Z})$で近似させたいとき, $$ D_{KL}(q({\bf Z})||p({\bf Z}|{\bf X})) $$ を最小化させることでその目的が達成されることが容易にわかるかと思います.
それを踏まえたうえで,モデルの対数周辺尤度$\ln p({\bf X})$(対数周辺尤度はしばしエビデンスと呼ばれます)を考えます.
また,この際一般の期待値に関しイェンセンの不等式が成り立つことを利用します
イェンセンの不等式 $$ f(\mathbb E[X])\leq \mathbb E[f(X)] $$
これを利用して
$$ \begin{eqnarray} \ln p({\bf X})&=&\ln\int p({\bf X},{\bf Z})d{\bf Z}\\ &=&\ln\int p({\bf X},{\bf Z})\frac{q({\bf Z})}{q({\bf Z})}d{\bf Z}\\ &=&\ln\mathbb E_{q}\left[\frac{p({\bf X},{\bf Z})}{q({\bf Z})}\right]\\ &\geq&\mathbb E_{q}\left[\ln\frac{p({\bf X},{\bf Z})}{q({\bf Z})}\right]\\ &=& \int q({\bf Z})\ln\frac{p({\bf X},{\bf Z})}{q({\bf Z})}d{\bf Z} \end{eqnarray} $$
この下界を$\mathcal L(q)$のようにして汎関数を定めます.$\mathcal L$は変分下界と呼ばれ,対数周辺尤度がエビデンスと呼ばれることからELBO(Evidence Lower BOund)と呼ばれます.
さて,つぎに対数周辺尤度からこの変分下界を引いてみます.
$$ \begin{eqnarray} \ln p({\bf X})-\mathcal L(q)&=&\int q({\bf Z})d{\bf Z}\ln p({\bf X})-\int q({\bf Z})\ln\frac{p({\bf X},{\bf Z})}{q({\bf Z})}d{\bf Z}\\ &=&\int q({\bf Z})\ln \frac{q({\bf Z})}{p({\bf Z}|{\bf X})}d{\bf Z}\\ &=&D_{KL}(q({\bf Z})||p({\bf Z}|{\bf X})) \end{eqnarray} $$
とKLダイバージェンスが導き出せます.周辺対数尤度は定数であるので,変分下界の最大化とKLダイバージェンスの最小化は等価であることが分かります.
3.2. 分解による近似分布の計算
上記の式変形で汎関数$\mathcal L(q)$が得られました.ここで,汎関数の極値を求めるにあたってオイラーの方程式*4を使います.
オイラーの方程式
汎関数 $$ I[y]\equiv\int \frac{f(x,y,y')}{q(y)}dx $$
の停留値を求めるには, $$ \frac{\partial f}{\partial y}-\frac{d}{dx}\left(\frac{\partial f}{\partial y'}\right)=0 $$
を解けばよい.
この場合は$y'$が$f$に含まれていないので単に, $$ \frac{\partial f(x,y)}{\partial y(x)}=0 $$
を解けばよいとといえます.
さて,このオイラーの方程式をこのモデルに用いて汎関数である変分下界の極値を求めます.
$q({\bf Z})$を排反な分布に分解して${\bf Z_i}(i=1,2,...,M)$と書くとします.このような分解された形を用いて近似を行うことは物理学の文脈では平均場近似(Mean-Field Approximation)と呼ばれ,特に事後分布をこの方法で近似する方法は変分ベイズ法(Variational Bayes)と呼ばれます.
$$ q({\bf Z})=\prod_{i=1}^{M}q_i({\bf Z_i}) $$
この下では変分下界は $$ \mathcal L(q)=\int \prod_{i=1}^{M}q_{i}({\bf Z_i})\left(\ln p({\bf X},{\bf Z})-\sum_{i=1}^{M}\ln q_{i}({\bf Z}_i)\right)d{\bf Z} $$ と書けます.簡単のために2つの場合を考えることにすると, $$ \mathcal L(q)=\iint q({\bf Z}_1)q({\bf Z}_2)\ln\frac{p({\bf X},{\bf Z})}{q({\bf Z}_1)q({\bf Z}_2)} d{\bf Z}_1d{\bf Z}_2 $$ となります.ここで,$q_2({\bf Z}_2)$を固定して考えると$q_1({\bf Z}_1)$の変分下界は,
$$ \mathcal L(q_1)=\int\left( \int q({\bf Z}_1)q({\bf Z}_2)\ln\frac{p({\bf X},{\bf Z})}{q({\bf Z}_1)q({\bf Z}_2)}d{\bf Z}_1\right)d{\bf Z}_2 $$
と式変形ができることから, $$ f(q_1,{\bf Z}_1)=\int q({\bf Z}_1)q({\bf Z}_2)\ln\frac{p({\bf X},{\bf Z})}{q({\bf Z}_1)q({\bf Z}_2)}d{\bf Z}_1 $$ とすると,変分法が適用でき, $$ \frac{\partial f(q_1,{\bf Z}_1)}{\partial q_1({\bf Z}_1)}=0 $$ を解くことで, $$ \ln q_1({\bf Z}_1)=\int q_2({\bf Z}_2)\ln p({\bf X},{\bf Z})d{\bf Z}_2+\text{const} $$ の時に極値を取ることが分かります. これは $$ \ln q_1^{*}({\bf Z}_1)=\mathbb E_{q_2}[\ln p({\bf X},{\bf Z})]+\text{const} $$ とも解釈できます.
$q_2$も同様, $$ \ln q_2^{*}({\bf Z}_2)=\mathbb E_{q_1}[\ln p({\bf X},{\bf Z})]+\text{const} $$
となります.
さらに,一般の$M$分割に対しても同様のことが言え,同時分布を自分以外の分解された近似分布で期待値を取ることで求めることができます.すなわち,$\mathbb E_{i\neq j}$を$i\neq j$であるすべての${\bf Z}_i$による分布$q_i$の期待値とみなすと $$ \ln q^{*}_{j}=\mathbb E_{i\neq j}[\ln p({\bf X},{\bf Z})]+\text{const} $$ のように最適解が与えられます.
変分ベイズ法はこの式を基礎として近似を行っていきます.$M$分割をおこなうことで$M$個の連立方程式が出来上がります.しかし,その方程式は他の因子$q_i({\bf Z}_i)(i\neq j)$の積分に依存しているので解析的に難しいため,各因子を適当な値で初期化して因子をそれぞれ,他の因子を固定して改良を重ねていくことで学習を行う,という手法がとられます.
4. 変分混合ガウス分布
(編集後記:非常に長くなりそうなので2回くらいに分ける.)
4.1. 事前分布の定義
変分ベイズが適用できる例としてクラスタリング問題が考えられます.
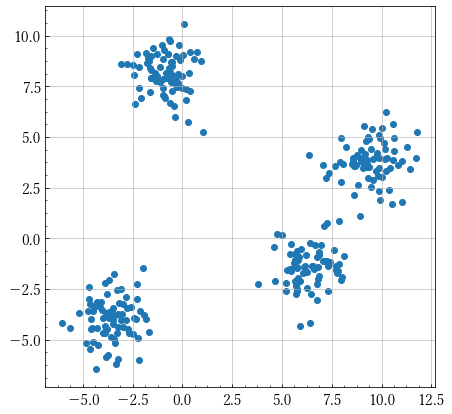
上のような分布に対して何個のクラスタリングに分けられるかという問題を考えるとき,K-Means法やEMアルゴリズムという決定論的な方法が考えられますが,ベイズ法を適用することで,特定のデータのみを説明する縮退が起こりえないことや,最適な要素(コンポーネント,クラスタ)数$K$を交差検証無しに求められるといった利点があります.
確率的なクラスタリングでは,この問題を次のようにモデル化します.
まず各観測値${\bf x}_n$に対して,対応するコンポーネントをOneHot化したベクトル${\bf z}_n$とします.データ数を$N$,コンポーネント数を$K$,次元数を$D$とすると,${\bf X}=\{{\bf x}_1,{\bf x}_2,...,{\bf x}_N\}$は$N\times D$,${\bf Z}=\{{\bf z}_1,{\bf z}_2,...,{\bf z}_N\}$は$N\times K$の行列となります.
ここで,混合ガウス分布は,コンポーネント数が$K$のとき,以下のように線形重ね合わせで表現することができることから,
$$ \sum_{k=1}^{K}\pi_k\mathcal N({\bf x}|{\bf \mu}_k,{\bf \Sigma}_k) $$
のように$\sum \pi_k=1,0\leq\pi_k\leq1$を満たす係数$\pi_k$でその混合比を表現することができます.
${\bf z}_n$はOneHotベクトル化されていることから,分布$p({\bf z}_n)$は, $$ p({\bf z}_n)=\prod_{k=1}^{K}\pi_k^{z_{nk}} $$ のように書き下すこともできます.したがって,分布$p({\bf Z}|{\bf \pi})$,$(\text{where}~{\bf \pi}:=\{\pi_1,\pi_2,...,\pi_k\})$は, $$ p({\bf Z}|{\bf \pi})=\prod_{n=1}^{N}\prod_{k=1}^{K}\pi_k^{z_k} $$ となります.また, $$ p({\bf x}_n|{\bf z}_n)=\prod_{k=1}^{K}\mathcal N({\bf x}_n|{\bf \mu}_k,{\bf \Sigma}_k)^{z_{nk}} $$ となることから,潜在変数が与えられたもとでの観測データのベクトルの条件付き分布は $$ p({\bf X}|{\bf Z},{\bf \mu},{\bf \Lambda})=\prod_{n=1}^{N}\prod_{k=1}^{K}\mathcal N({\bf x}_n|{\bf \mu}_k,{\bf \Lambda}_k^{-1})^{z_{nk}} $$
となります.ただし,共分散行列ではなく精度行列${\bf \Lambda}$(共分散行列の逆行列)を計算の簡単化のために用いています.
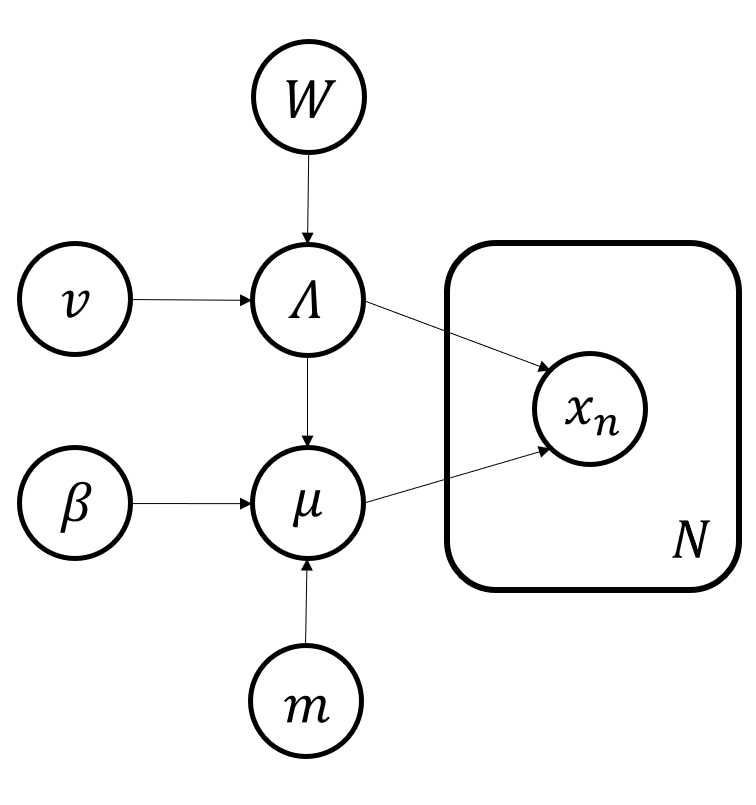
次にベイズ的アプローチを導入するため,パラメータ${\bf \pi},{\bf \mu},{\bf \Lambda}$に事前分布を導入します.まず,$p({\bf \pi})$は多変量のベータ分布に相当するディリクレ分布を仮定します*5.
$$ p({\bf \pi})=\frac{\Gamma(\sum \alpha_{0k})}{\prod\Gamma(\alpha_{0k})}\prod_{k=1}^{K}\pi_{k}^{\alpha_{0k}-1} $$ ただし,${\bf \alpha_{0}}$はすべての要素$\{\alpha_{0k}\}$が同じ値のベクトルとした.また上の式の係数はディリクレの正規化定数と呼ばれ,$C({\bf \alpha}_0)$のように表記する.
次に分布$p({\bf \mu},{\bf \Lambda})$は,平均と分散が未知なのでガウスウィシャート分布が適します.
$$
p({\bf \mu},{\bf \Lambda})=\prod_{k=1}^{K}\mathcal N({\bf \mu}_k|{\bf m}_0,(\beta_0{\bf \Lambda_k})^{-1})\mathcal W({\bf \Lambda_k}|{\bf W},\nu_0)
$$
(以下ポエム)
残りは次回に回すことにします.この例はPRMLでもなかなか長く歯ごたえのある所だと思うので念入りにやっていきたい.いままでVAEなどについても理解が及ばない点が多く,変分下界の存在意義とかそういったものを理論立てて学べる良い教材だった.
次回