Large Scale GAN Training for High Fidelity Natural Image Synthesis(BigGAN)::10/6

https://arxiv.org/pdf/1809.11096.pdf

-1. AbstractのAbstract

緻密に色々試したら，つぎは計算機で殴ろうな！！

0. Abstract

いわゆる，BigGANという名前で，少し話題になっているGANです．DeepMindのインターンの成果物らしく自己アテンションを組み込んだSelf-Attention GANをベースに様々な最適化手法が取り込まれているようです．Appendix Gにあるように「こうしたら悪い結果が出た」というのを掲載しているので実装等の際には非常に有用となるかと思います．チャンネル数とバッチサイズの大小と精度についても述べられており，双方ともに上げた方が良い結果が望めるとのこと(やはり計算資源のデカさこそ正義らしい)．潜在変数$z$のサンプリング範囲をあらかじめ決めておいて，その範囲外のサンプルを切り捨てる"Transaction Trick"を使用することで多様性を実現しているようです．Scoreとしては従来のState-of-the-art(SoTA)であるInception Score(IS)とFIDの値52.52,18.65よりも大幅に高精度の166.3,9.6を記録したという驚きの結果が出ています．

1. Introduction

GANの画像生成で往々にして話題になるのは生成画像のそっくり度(Fidelity)と多様性(Variety)です．

以下の3つを考慮することでこれの更新を達成しようと試みたようです．

GANはスケーリングにより大きな影響を受ける．つまるところ，バッチサイズ，パラメータを4倍程度にすることでGANは大幅に利益を受けることを示す．計算資源こそ正義．加えて，スケーラビリティを向上させる簡単なGANアーキテクチャを導入し，また，正規化手法を新たに導入しコンディショニングを改善させることで，大幅なパフォーマンスの向上を図った．
モデルのFidelityとVarietyのトレードオフを細かに制御ができる単純な"Truncation Trick"を導入した．
大規模なGANを訓練させえる際に特有な不安定性を考察した．経験的にそれらを特徴付けすることで，既存技術と新規技術を融合させることでこの不安定性がある程度軽減できることを立証した．

3. Scaling Up GANs

この節では，GANが大きなバッチサイズとパラメータに対して利益を得るために必要な，GANのトレーニングのための手法を考察するようです．

SA-GAN(Zhang et al.,2018¹)がベースで，GANの損失関数としてはヒンジ関数(Lim & Ye,2017² )を利用したらしい．$G$に分類の情報を与えるために，class-conditional Batch Norm(Dumoulin et al.,2017³)を採用し，$D$にはprojection(宮戸(PFN)&小山(立大),2018⁴ )を採用．Spectral Norm(宮戸,2018⁵)を$G$にも適用(SA-GANと同じ手法)を取ったが，学習率を半分にし，$D$の学習と$G$の学習の回数の比を$2:1$にした．

また，PGGAN(Karras et al.,2018⁶)でも取られている$G$の重みを動的に制御するシステムを減衰率$0.9999$で適用し，重みの初期化は直交初期化(Orthogonal Initialization/Saxe et al.,2014⁷)を使った．

計算資源は昨今話題のTPU v3(Tensor Processing Unit/Google,2018)を使った．さらに512四方の大きな画像でも，PGGANのような逐次的に高解像度へと発展させていく機構が必要ないと言えたらしいです．

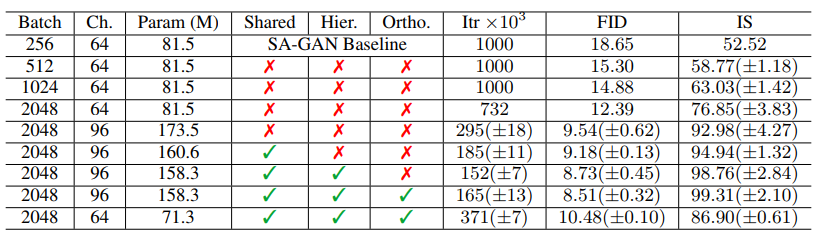
まず，Batch Sizeをもとの論文(SA-GAN)の$256$から2,4,8倍へと大きくさせていた結果Batch Sizeに応じてスコアが漸増しており，計算資源こそが正義ということが分かります．Batchが大きいほど入力の多様性が増えるわけですので所謂モード崩壊⁸が生じにくくなると単純に推測ができるようです．また，Batch Sizeの増加は単純にBatch par Epochが減少するので訓練時間がより短くなるという嬉しい副作用があります．しかしながら，場合によっては学習が失敗してしまうという結果が観測されたようで，上記の結果は学習の崩壊前の最善のウェイトを使った際の結果とのことです．学習の安定化についての考察は第4節にて考察するそうです．

次に各々のレイヤのチャンネル数を150%($64\rightarrow 96$)にしてパラメータ数を大体倍にした際もスコアの上昇がみられたようです．

また，$G$で使われている条件付きBatch Normは多くのパラメータを含んでいる．そこで，各レイヤで埋め込みを行う(宮戸,2018[^4])のではなく，各々のレイヤのバイアスとゲインを線形投影させる，共有埋め込み(Shared Embedding)を用いてパラメータと学習時間(＝計算コスト)を削減させた．

さらに，はじめの層以外にノイズを入力させる技法を採用した．この目的としては潜在空間を利用して異なる解像度や異なる階層のレベルで影響を及ぼすことが目標らしい⁹.

3.1. "Truncation Trick"によるVarietyとFidelityのトレードオフ

GANは入力潜在変数分布$p(z)$を任意の分布に設定することができるが，ほとんどのGANの論文ではたいてい正規分布$\mathcal{N}(0,1)$や，一様分布$\mathcal{U}[-1,1]$などからノイズを生成している．この事前分布の選定によるパフォーマンスの違いをオマケEにてまとめてあるようだ．

数々の事前分布で実験を行ったところ，驚くべきことに，学習時とサンプリング(予測)時で異なる分布からサンプリングしたほうが良い結果となることが分かったようだ．学習時には$z\sim\mathcal{N}(0,1)$で，生成時には打切り正規分布(Truncated Normal:最頻値からの特定範囲外のサンプルを棄却した正規分布)を用いた際に最も良い結果となることが観測された．このテクニックをTruncation Trickと呼ぶことにする．

打切りの閾値は生成画像の多様性とそれっぽさに大きく影響を与える．上の図は閾値を$2,1.5,1,0.5,0.04$¹⁰とした場合である．

打切りの閾値を操作することで，事後的かつ詳細に(Fine-Grained Post-Hoc)生成画像の多様性とそれっぽさを変えることが可能となる．

実際にこのトレードオフを可視化すべくISとFIDという評価指標を用いて実験を行ったようだ．

ISはInceptionモデルで識別しやすい画像でかつ，識別されるラベルの多様性が豊富なほど¹¹高スコアを記録するものであり，FIDはGANの生成する画像の品質を評価する¹²もので，真の分布の画像集合と再現分布の画像集合間の距離を評価するものであるので，低スコアである方が望ましい．

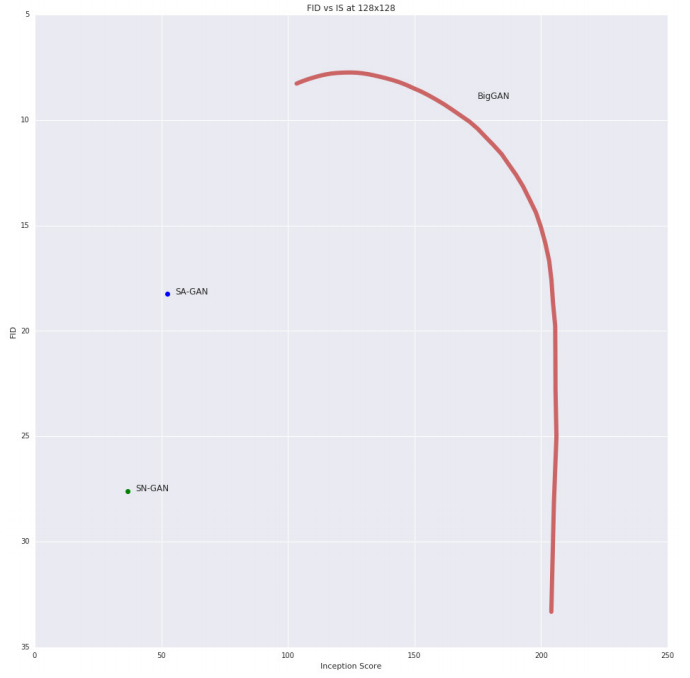
(実際に評価した図はオマケDの図16に載っている)

しかし，大きなモデルの中には打切りがうまく作用せずサチった(Saturated)画像を生成してしまう場合があるようだ(Saturation Artifact)．これに対応するために，$G$を平滑化させるように条件付けし，切り捨てに対する順応性を上げる必要性，つまりは，潜在変数$z$の全空間に置いて良好な出力に射影されるようにさせる．これを達成すべく，直交正則化(Orthogonal Regularization,Brock et al,2017[^6])を適用した: $$ R_{\beta}(W)=\beta||W^{T}W-I||^{2}_{F} $$ ただし，$||\cdot||_{F}$は行列の要素ごとの平方和の平方根であるフロベニウスノルムで，$W$は重みパラメータ，$\beta$はハイパーパラメータである．この正則化は制限が強すぎる[^4]ことが指摘されており，そのため，より緩い制約となるような正則化項を探索したところ次のような正則化項が最も有用であることがわかった． $$ R_{\beta}(W)=\beta||W^{T}W\odot({\bf 1}-I)||_{F}^{2} $$ ただし，$\odot$は行列のアダマール積(要素ごとの積)で，${\bf 1}$は全要素が1である行列である．

$\beta=10^{-4}$程度の軽い正則化を課したところ，パフォーマンスの向上が見受けられた．

4. 分析

4.1. Characterizing Instability: Generator

GANの分析の際は簡単な分布を用いて考察を行うことが多いが，ここでは大規模の問題を直接解析したいので，Odena et al(2018)¹³ でとられているように，学習中の重みと勾配，損失を監視して学習の崩壊する要因となりうる予兆となる指標を探すことにする．

観測の結果各重み行列の第三位までの特異値$\sigma_0,\sigma_1,\sigma_2$が，崩壊の観測に対して有用であることが明らかとなった．行列の特異値は宮戸 et al.(2018)[^4]で使われている冪乗法を拡張したAlrnoldiの反復法(Golub et al.,2000¹⁴ )を用いて計算できる．

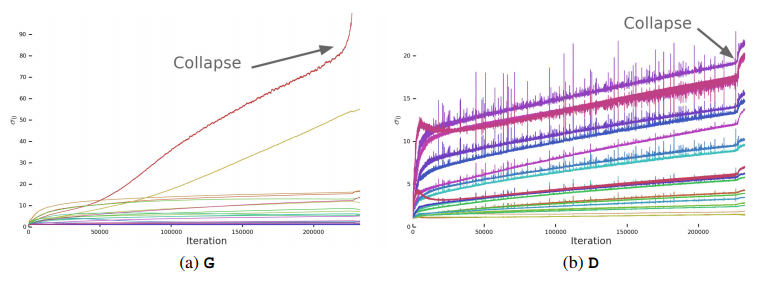
実際の学習の際にこの(Spectral Normを適用する前の)特異値の変化をプロットしたところ学習崩壊の際に特異値が急に爆発することが観測された．

この病的なふるまいが，崩壊の原因なのか症状なのかを究明するため，$G$に対してスペクトル爆発を明示的に抑制させる為の追加の条件を課すことにしたようだ．

スペクトル爆発を制御する方法としては，重み行列$W$をとして，第一特異ベクトルと特異値$u_0,v_0,\sigma_0$として，$\sigma_0$に対してクランプされる値を$\sigma_{clamp}$とすると，重みを次のようにして更新する． $$ W=W-\max(0,\sigma_0-\sigma_{clamp})v_0u_{0}^{T} $$ ここでクランプ値は次のようにして設定することにする．

単に固定値$\sigma_{reg}$を設定してクランプする
第二特異値$\sigma_1$に対する比$r\cdot sg(\sigma_1)$．ただし，$sg(\cdot)$は正則化により$\sigma_1$を増加させないようにするための勾配に対する停止操作である¹⁵

クランピングである程度のパフォーマンス改善や，爆発防止が見込める場合があるが，完全に学習の崩壊の防止を行うことはできないようだ．

スペクトルノルムは学習安定化のための重要な要素であるが，現在のテクニックではうまく安定化させることは難しいようだ(悲しい)．

4.1の補足: 特異値

特異値分解は，正方行列にのみ適応可能な固有値分解を縦横が一致しない一般の矩形行列にたいして適用できるように拡張させたものであるといえます．

特異値分解は行列$M\in K^{m\times n}$(体$K$は実数や複素数を考える)をユニタリ行列$U\in K^{m\times m},V\in K^{n\times n}$と，半正定値行列$MM^{\star}$(ここで$A^{\star}$は$A$の転置+複素共役行列(随伴行列ともいう))の正の固有値の平方根$\sigma_1\geq\sigma_2\geq...\geq\sigma_r>0$が存在して，$q=\min(m,n),\sigma_{r+1}=...=\sigma_{q}=0$と置いて，$\Delta=\text{diag}(\sigma_1,\sigma_2,...,\sigma_q)$として，$\Sigma\in K^{m\times n}$を左上に$\Delta$を置いて，残りの部分を0埋めした行列として， $$ M=U\Sigma V^{\star} $$ という形に分解することをいい，$\sigma_r$は特異値と呼ばれます．

固有ベクトルが正規直交基底となったことと同様に特異値分解でも行列$V$が入力空間における正規直交基底となり，$U$が出力空間における正規直交基底と等しいといえ，$\Sigma$は成分のゲインであると考えることができる．基本的に特異値は降順に並べることが多く，この場合$\Sigma$が一意に定まることが知られています．

上記特性から特異値は $$ \begin{eqnarray} Mv&=&\sigma u\ M^{\star}u&=&\sigma v \end{eqnarray} $$ が成り立つ$u,v$組に対応する$\sigma$であるといえ，$u$を左特異ベクトル，$v$を右特異ベクトルと呼ばれます．

特異値分解を行うメソッドはnumpyに実装されておりnp.linalg.svg(Matrix)を実行することで返り値として$U,\Sigma,V^{\star}$を得ることができます．

たとえば， $$ A=\left[ \begin{array}{ccc} -\sqrt{2}^{-1} & 1 & -1\\ -\sqrt{2}^{-1} & -1 & 1 \end{array} \right] $$ の特異値は $$ \Sigma=\text{diag}(2,2) $$ のように表すことができ，

import numpy as np
A = np.array([[-(2)**(.5), 1, -1], [-(2)**(.5), -1, 1]])
U, s, V = np.linalg.svd(A)

とすることで，実際に特異値分解を行うことができます．

print(U)
print(s)
print(V)
# [[-1.00000000e+00 -2.22044605e-16]
#  [-2.22044605e-16  1.00000000e+00]]
# [2. 2.]
# [[ 7.07106781e-01 -5.00000000e-01  5.00000000e-01]
#  [-7.07106781e-01 -5.00000000e-01  5.00000000e-01]
#  [-1.75725255e-16  7.07106781e-01  7.07106781e-01]]

さて，特異値を実際に近似で求めるアルゴリズムの中で，Spectral Normの論文で紹介されているものとして冪乗法(Power Method)があります．冪乗法は以下からなるアルゴリズムです

アルゴリズム 1:冪乗法

入力:$A\in K^{m\times n}$と反復回数$N$

出力:最大(第一)特異値$s$¹⁶ ,とその左及び右の特異ベクトル$u,v$

let $q\in K^{n}, \text{where,}~q_i \leftarrow \mathcal{N}(0,1),||q||_2=1$

for $i$ in $0..N$:

$~~~~~~~~q\leftarrow A^{T}Aq$

$v \leftarrow q/||q||_2$

$s\leftarrow ||Av||_2$

$u\leftarrow Av/s$

return $u,s,v$

これをPythonで実装させると，

def power_method(A, num_iter=1):
    q = np.random.normal(size=A.shape[1])
    q = q/np.linalg.norm(q)
    for i in range(num_iter):
        q = A.T.dot(A).dot(q)
    v = q / np.linalg.norm(q)
    s = np.linalg.norm(A.dot(v))
    u = A.dot(v)/s
    return u, s, v

このようになり¹⁷，実際に先ほどの例を実行させると，

print(power_method(A, 5))
# output:
# (array([ 0.6678161 , -0.74432631]),
# 1.9912766893959086,
# array([0.07617649, 0.70299157, 0.07617649, 0.70299157]))

と，およそnumpyの実行結果と一致していることが確認できます．

対して，この論文で紹介されているArnoldi法の実装はコレ¹⁸が詳しいので同様に実装することができます．

4.2. Characterizing Instability: The Discriminator

$G$と同様に$D$に対してもスペクトルノルムの分析を行い，制約を課して学習を安定させることを考える．

$D$の特異値は$G$に比較して，ノイズが多い傾向にあり，また崩壊時は$G$と違って値が爆発的に増加するのではなく漸増量が増加する傾向にある．

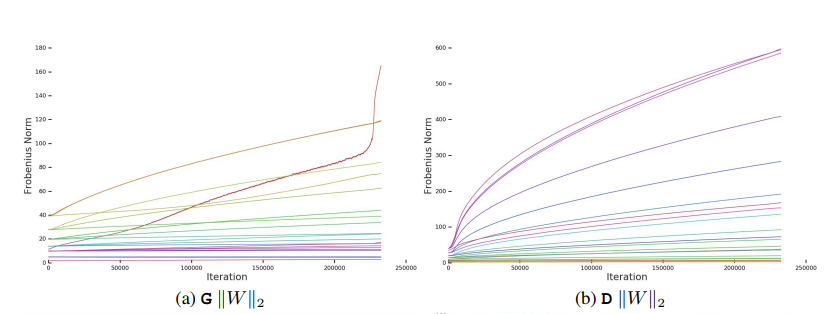
ところどころ$D$の特異値に観測される尖頭値についてまず考察をする．この尖頭値から，周期的に非常に大きな勾配を受け取るようなことを示唆しているように思えるが，$D$のフロベニウスノルムが滑らかであることを考えると，この尖頭値現象はいくつかの主位特異ベクトル方向に集中しているといえる．つまり，尖頭値では$G$が$D$を激しく攪乱させるような画像を生成されたが故の敵対的プロセス下での最適化の結果によるものだと仮定できる．

このスペクトルノイズが不安定性と関連があるかどうか調べるために，$D$のヤコビアンを明示的に制限するような勾配罰則を適用して正則化する．この実験ではMescheder et al.(2018)¹⁹の，$R_1$ゼロ中心勾配罰則(Zero-centered Gradient Penalty)を導入した．

$$ R_1:=\frac{\gamma}{2}\mathbb{E}_{p_{\mathcal{D}}(x)}[||\nabla D(x)||_F^{2}] $$

$\gamma$を$10$とすることで学習が安定化し，スペクトルの平滑さが向上したがパフォーマンスは著しく低下した．特にIS(多様性)の方のスコアが45%ほど落ち込む結果となった．むろん$\gamma$を緩和することでパフォーマンスは向上するが次第にスペクトルの尖頭が目立つようになり始め，$\gamma=1$でもISは20%のパフォーマンス低下が生じるという結果となった．

同様の実験を直交正規化[^6],DropOut²⁰,L2正則化で行ったが同様の結果となった．

5. 実験

ImageNetとJET-300Mで実験を行ったようです．

ImageNet

結果が左から

Truncation Trickを行わなかった場合のスコア
FIDを最小化したときのスコア(最大精度)
ISの検証セットを利用したときのスコア(汎化の客観性)
ISを最大化したときのスコア(最大多様性)

となっている．

JET-300M

256四方の場合における実験結果のようです．

オマケにはパラメータ等調整の際の試行錯誤の結果が載っており再現実験等をする場合非常にありがたいかもしれませんが，512四方の画像をチャネル96，バッチ数2048で実行できる計算機でぶん殴る必要があるでしょう．つらい．

Self-Attention Generative Adversarial Networks https://arxiv.org/abs/1805.08318 ↩
Geometric GAN,https://arxiv.org/abs/1705.02894 ↩
A Learned Representation For Artistic Style,https://arxiv.org/pdf/1610.07629.pdf ↩
cGANs with Projection Discriminator,https://arxiv.org/abs/1802.05637 ↩
Spectral Normalization for Generative Adversarial Networks,https://arxiv.org/abs/1802.05957 ↩
Progressive Growing of GANs for Improved Quality, Stability, and Variation,https://arxiv.org/abs/1710.10196 ↩
Exact solutions to the nonlinear dynamics of learning in deep linear neural networks,https://arxiv.org/abs/1312.6120 ↩
$G$が最頻(mode)単峰分布のみをめちゃくちゃよい精度で生成するように学習して多様性のある画像が生成されなくなる現象↩
ここがいまいち理解できなかった．初期層以外にノイズを入力することによる利点が何かを別途別文献参照して考察したい↩
図の個数と閾値の数が合ってない? ↩
http://bluewidz.blogspot.com/2017/12/inception-score.htmlこの記事が詳しい ↩
http://bluewidz.blogspot.com/2017/12/frechet-inception-distance.html同じくこの記事が詳しい↩
Is Generator Conditioning Causally Related to GAN Performance?https://arxiv.org/abs/1802.08768 ↩
Journal of Computational and Applied Mathematics,(検索結果がArnoldiしか出ないが原文ママである,http://shnya.hatenablog.jp/entry/2016/03/12/100507が詳しい)↩
どういう操作をすればいいのかいまいちわかりませんでした…↩
行列の最大の特異値のことは行列のスペクトルノルム(Spectral Norm)といわれるものです．行列に対する$L_2$ノルムであり，$||A||_{2}=(Maximum~Singular~Value)=\max_{||x||_{2}\neq0}||Ax||_2/||x||_2$であることが示されています．特異値が入力に対するゲインと考えるとSpectral Normは入力を極端に大きくスケーリングしないように調整している．とでもいえるのでしょうか？(←この私の考え方が正しいかどうかは判断しかねますが)↩
https://blog.tsurubee.tech/entry/2017/11/05/225803を参照にした．↩
http://ry0u.github.io/post/2018-06-16-arnoldi-and-eigenvalues/↩
Which Training Methods for GANs do actually Converge? https://arxiv.org/abs/1801.04406 ↩
Dropout: A Simple Way to Prevent Neural Networks from Overfitting http://jmlr.org/papers/volume15/srivastava14a.old/srivastava14a.pdf ↩