統計的学習の基礎 2章のメモ
統計的学習の基礎を買ったのでそのメモを公開します.どこか,変な所がございましたらコメントをお願いいたします!

- 作者: Trevor Hastie,Robert Tibshirani,Jerome Friedman,杉山将,井手剛,神嶌敏弘,栗田多喜夫,前田英作,井尻善久,岩田具治,金森敬文,兼村厚範,烏山昌幸,河原吉伸,木村昭悟,小西嘉典,酒井智弥,鈴木大慈,竹内一郎,玉木徹,出口大輔,冨岡亮太,波部斉,前田新一,持橋大地,山田誠
- 出版社/メーカー: 共立出版
- 発売日: 2014/06/25
- メディア: 単行本
- この商品を含むブログ (6件) を見る
2.3. 最小二乗法と最近傍法
最小二乗法
統計的にデータを解析したい際に,昔からよく取られる有用な方法の一つに,線形モデルによる近似がある.線形モデルとは入力$\boldsymbol{x}^ T=(x_1,x_2,...,x_p)$に対して出力$y\in \mathbb{R}$を $$ \hat{y}=\hat\beta_0+\sum_{j=1}^ {p}\hat\beta_jx_j $$ のように線形和で予測する方法である.$x_0=1$とすることでバイアス項を一つにまとめることができて $$ \hat y=\boldsymbol{x}^ T\hat{\boldsymbol{\beta}} $$ のようにベクトル表記で簡潔に表すことが可能である.ただし上の$\boldsymbol{x}^ T,\hat{\boldsymbol{\beta}}$は$p+1$次元である.
最小二乗法は,このアプローチに対して,各点の残差二乗和(RSS)を最小化するように適切な$\boldsymbol{\beta}$を学習する手法である.
$$ \text{RSS}(\boldsymbol{\beta})=\sum_{i=1}^ {N}(\hat{y}_i-\boldsymbol{x}_i^ T\boldsymbol{\beta})^ {2} $$
これは$X\in \mathbb{R}^ {N\times(p+1)},\boldsymbol{\beta}\in \mathbb{R}^ {p+1},\boldsymbol{y}\in \mathbb{R}^ {N}$のように行列を用いて表記すると, $$ \text{RSS}(\boldsymbol{\beta})=(\boldsymbol{y}-X\boldsymbol{\beta})^ T(\boldsymbol{y}-X\boldsymbol{\beta}) $$ のようにも表記することが可能である.
$\boldsymbol{\beta}$で偏微分すると
$$ \newcommand{\v}[1]{\boldsymbol{#1}} $$
$$ \begin{eqnarray} \frac{\partial}{\partial \boldsymbol{\beta}} \text{RSS}(\boldsymbol{\beta})&=&\frac{\partial}{\partial \boldsymbol{\beta}}(\boldsymbol{y}^ T\boldsymbol{y}-\boldsymbol{\beta}^ TX^ T\boldsymbol{y}-\boldsymbol{y}^ TX\boldsymbol{\beta}+\boldsymbol{\beta}^ TX^ TX\boldsymbol{\beta})\\ &=&-X^ T\boldsymbol{y}-\boldsymbol{y}^ TX+(X^ TX+(XX^ T)^ T)\boldsymbol{\beta}\\ &=&-2X^ T(\boldsymbol{y}-X\boldsymbol{\beta}) \end{eqnarray} $$
となり,この式=0とときの方程式の解$\hat{\boldsymbol{\beta}}$で極値をとることが分かる.この方程式は正規方程式と呼ばれる.この解は$X^ TX$が特異でない限り,解くことが可能で $$ \hat{\boldsymbol{\beta}}=(X^ TX)^ {-1}X^ T\boldsymbol{y} $$ という解になる.
実装例
import numpy as np import matplotlib.pyplot as plt class LeastSquare(): def fit(self, X, y): self.X = np.hstack([np.ones((X.shape[0],1)), X]) self.w = np.linalg.inv(self.X.T.dot(self.X)).dot(self.X.T).dot(y) def predict(self, X): return X.dot(self.w) # トイデータの作成 X = np.concatenate([np.random.normal((-2, 2), (4, 4), (60, 2)), np.random.normal((2, -1), (4, 4), (60, 2))]) y = (np.arange(0, 120)//60).astype(np.int32) model = LeastSquare() model.fit(X, y) w = model.w f = lambda x: (w[0] + w[1] * x - 0.5) / -w[2] plt.scatter(X[:, 0], X[:, 1], c=y) t = np.linspace(-10, 10) plt.plot(t, f(t))

最近傍法
k最近傍法は$\hat y$を予測する際,入力に対する最も近い訓練データ$k$点の値を利用する.アルゴリズムは単純で,入力$x$に最も近い点から$k$個の点$N_k(x)$を選んでその訓練ラベルの平均を算出して予測出力とする. $$ \hat{y}=\frac{1}{k}\sum_{x_i\in N_k(x)}y_i $$ 01分類問題であればこの値が0.5より大きいか小さいかで分類を行う.
むろん,kが1に近づくにつれて誤分類が少なくなるため,訓練誤差は少なくなるが,汎化性能が低下してしまう.
また,k最近傍法は,一見パラメータ数が$k$個のみのように思えるが,有効パラメータ数と呼ばれるものがk最近傍法の場合,$N/k$となることが知られている.すなわち,$k$が増加するにしたがって有効パラメータ数は減少する.
実装例
class KNN(): def __init__(self, k=3): self.k = k def fit(self, X, y): self.X = X self.y = y def predict(self, X): dists = np.array([self._distance(p, X) for p in self.X]) nearpoints = dists.argsort(axis=0)[:self.k, :] return self.y[nearpoints].mean(axis=0) # ユークリッド距離 def _distance(self, x0, x1): return ((x0 - x1)**2).sum(axis=1) k = 20 model = KNN(k=k) model.fit(X, y) plot_decision_regions(X, y, model, title='k=%d' % k)
(plot_decision_regionsは本質ではないのでここに格納してあります)
- k=20の場合
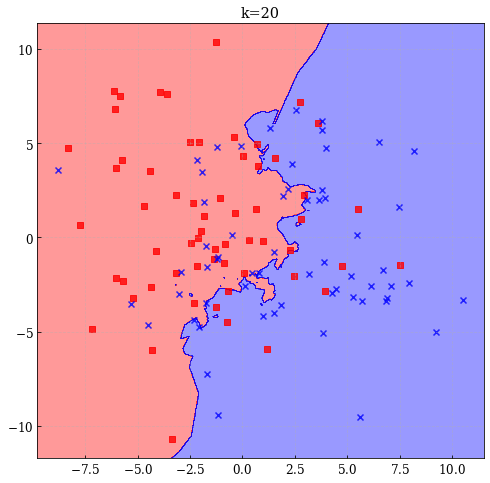
- k=1の場合
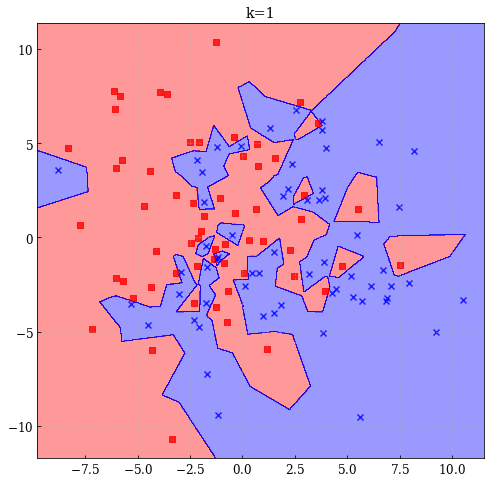
最小二乗法は決定境界が滑らかであり,当てはめの結果も安定しているが,線形であるという仮定に大きく依存している.一方で最近傍法は生成過程に対して厳密な仮定を置いていないため任意のデータに対してうまく適合するように思える.しかし,決定境界が曲がりくねった複雑なものになりやすいものとなるという問題点もある.
統計学の用語では前者の最小二乗法のようなモデルはバイアスが大きいモデルといわれ,最近傍法のようなモデルはバリアンス(分散)が大きいモデルであると呼ばれる.
2.4. 統計的決定理論
入力確率変数$X\in \mathbb{R}^ p$,出力確率変数$Y\in\mathbb{R}$が,同時確率分布$P(X,Y)$に従うような場合を考える.このようなときに出力を予測する関数$f$を予測させるためにはどうすればよいか.
理論的に考察するため,予測に関する罰則$L$を定義することは有用で.二乗誤差損失 $$ L(Y,f(X))=(Y-f(X))^ 2 $$ はその中でもよく用いられる.この二乗誤差損失を用いると,関数$f$はどう定義されるのかを考察する.
定量的に扱うため,この二乗誤差損失の期待値である期待二乗予測誤差(EPE)を考えよう. $$ \begin{eqnarray} \text{EPE}(f)&=&\mathbb{E}\left[(Y-f(X))^ 2\right]\\ &=&\int[y-f(x)]^ 2P(dx, dy)\\ &=&\iint[y-f(x)]^ 2P(x,y)dxdy\\ &=&\int\left(\int[y-f(x)]^ 2P(Y=y|X=x)dy\right)P(x)dx\\ &=&\int\mathbb{E}_{Y|X}[(y-f(x))^ 2|X=x]P(X=x)dx\\ &=&\mathbb{E}_X\mathbb{E}_{Y|X}[(y-f(x))^ 2|X] \end{eqnarray} $$ から,それぞれの入力$x$に対して最小化を行えばよく, $$ f(x)=\arg\min_c\mathbb{E}_{Y|X}[(y-c)^ 2|X=x] $$ となる.よって $$ \begin{eqnarray} \arg\min_c\mathbb{E}_{Y|X}[(y-c)^ 2|X=x]\Rightarrow \frac{\partial}{\partial f}\int[y-f]^ 2P(Y=y|X=x)dy&=&0\\ \int\frac{\partial}{\partial f}[y-f]^ 2P(Y=y|X=x)dy&=&0\\ -2\int yP(Y=y|X=x)dy+2f\int P(Y=y|X=x)dy&=&0\\ -\mathbb{E}_Y[Y|X=x]+f&=&0\\ f(x)&=&\mathbb{E}_Y[Y|X=x] \end{eqnarray} $$ となる.最後の関数は回帰関数と呼ばれる.
すなわち,二乗誤差を考慮した状況下では$X=x$のもとでの最良の予測は条件付き期待値に等しいといえる.
最近傍法は,訓練データからこの期待値を $$ \hat{f}(x)=\text{Ave}(y_i|x_i\in N_k(x)) $$ と期待値を標本平均に,その点直接ではなく近傍領域へと緩和して,直接近似している.
$k,N\rightarrow\infty,k/N\rightarrow0$のもとでは実際$\hat{f}(x)\rightarrow \mathbb{E}_Y[Y|X=x]$となることが証明されている.しかしながら,多くのデータを集めることは困難であり,線形性等の構造上の仮定がデータに対して満たしていればそのモデルの方が安定した推定が可能であることがわかる.
また,近傍領域を考慮するk最近傍法は次元数$p$が大きくなるにつれて高次元特有の不利益をうけてしまうことが知られている.
最小二乗線形回帰の場合は$f(\boldsymbol{x})\approx \boldsymbol{x}^ T\boldsymbol{\beta}$と近似できると仮定することで,上の期待二乗予測誤差の式に代入しそれを最小化する解$\boldsymbol{\beta}$を求めるべく偏微分することで $$ \begin{eqnarray} \frac{\partial}{\partial \boldsymbol{\beta}}\text{EPE}(f)=\frac{\partial}{\partial \boldsymbol{\beta}}\iint[y-\boldsymbol{x}^ T\boldsymbol{\beta}]^ 2P(x,y)dxdy&=&0\\ \iint-2\boldsymbol{x}(y-\boldsymbol{x}^ T\boldsymbol{\beta})P(x,y)dxdy&=&0\\ \iint(y\boldsymbol{x}-\boldsymbol{x}\boldsymbol{x}^ T\boldsymbol{\beta})P(x,y)dxdy&=&0\\ \mathbb{E}[XY]-\mathbb{E}[XX^ T]\boldsymbol{\beta}&=&0\\ \boldsymbol{\beta}&=&(\mathbb{E}[XX^ T])^ {-1}\mathbb{E}[XY] \end{eqnarray} $$ 以上をまとめると最小二乗法は線形関数でうまく回帰関数を近似できると仮定し,k最近傍法は局所的な定数関数でうまく近似できると仮定しているという点が異なるといえる.
また,ここまで$L_2$誤差損失のみを考えてきたがこれを$L_1$誤差損失へと置き換えた場合,最良を示す回帰関数は何になるであろうか.これは,条件付き中央値へとなることが知られている.
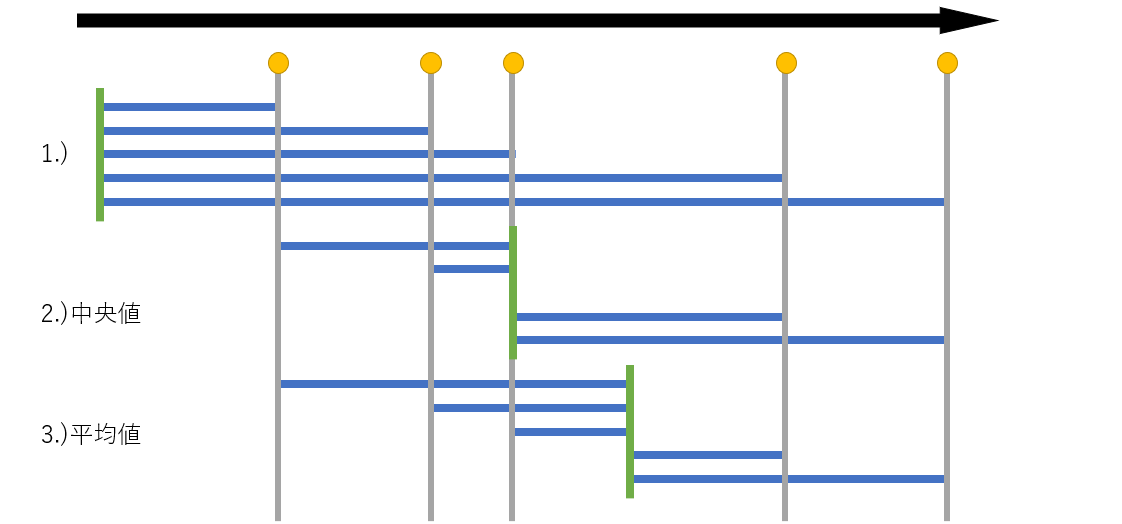
中央値は左に存在する点の数と右に存在する点の数が等しくなるような点が中央値であるので,かりに上の図の緑線が中央値より右にずれた場合,中央値とそれより左にある点は右方向に余計な損失が生まれてしまう.このことから $$ \hat{f}(x)=\text{median}(Y|X=x) $$ が回帰関数となる.
離散の場合はカテゴリ型の変数を$G$として,そのカテゴリが集合$\mathcal{G}$のうちのいずれかの値を取ると仮定する.カテゴリ数を$K$とする($K=\#\mathcal{G}=\text{card}(\mathcal G)$)この時の損失関数は,対角成分が0でそれ以外が非負の$K\times K$行列$L$によって与えられる.損失としては多くは0,1の損失が取られる($L\in\{0,1\}^ {K\times K},\text{tr}~L=\boldsymbol{0}$).
このとき,期待予測誤差は $$ \text{EPE}=\mathbb{E}[L(G,\hat{G}(X))] $$ として与えられる.ただし,$L(k,l)$はクラス$\mathcal G_k$を誤って$\mathcal G_l$へと分類した時の罰則である.
これは $$ \text{EPE}=\mathbb{E}_X\sum_{k=1}^ {K}L(\mathcal{G}_k,\hat{G}(X))P(\mathcal G_k|X) $$ とあらわすことができ,連続の場合と同様に $$ \hat{G}(x)=\arg\min_{g\in\mathcal G}\sum_{k=1}^ {K}L(\mathcal G_k,g)P(\mathcal G_k|X=x) $$ と変形できさらに01損失の場合は $$ \hat{G}(x)=\arg\min_{g\in \mathcal G}[1-P(g|X=x)] $$ と単純化できる.
この解は,条件付き確率を用いて最も確からしいクラスへと分類する妥当なものとなっており,そのようなモデルをベイズ分類器などと呼ばれている.
2.5. 高次元での局所的手法
$p$次元単位超立方体に対して,データ点が一様に分布していると考える.ある頂点からの近傍を単位超立方体内の部分超立方体と定義し,$p$を変化させたときの部分超立方体の一辺の長さと体積の割合を考えよう.
近傍データ数が全データのうち,割合$r$だけ含んでいるとしたときの近傍の部分超立方体の長さの期待値は$e_p(r)=r^ {1/p}$となるため,$p=10$の場合を考えてみると,$e_{10}(0.01)=0.63, e_{10}(0.1)=0.80$である.
これは,10次元のパラメータ空間において入力データ点に対する全データ点の1%や10%の近傍を考慮するためには,入力変数に対してそれぞれ63%,80%の空間を近傍とみなさなければならないということを示している.
plt.figure(figsize=(6, 6)) for p in [1, 2, 3, 10, 100]: t = np.linspace(0, 1, 200) y = t ** (1 / p) plt.plot(t, y, label='p=%d' % p) plt.xlabel('体積の割合') plt.ylabel('距離') plt.legend()
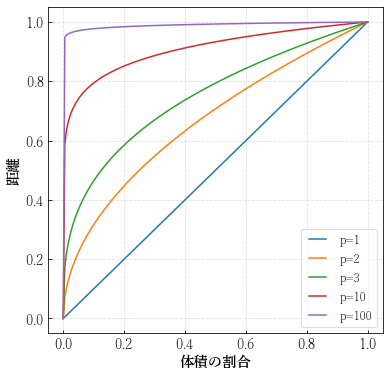
また,高次元空間においてはあらゆる点がデータの中心から離れて分布してしまうという問題がある.
データ点$\mathcal{D}=\{\boldsymbol{x_1},\boldsymbol{x_2},...\boldsymbol{x_N}\}$が$p$次元の超球内に一様分布している場合を考える.
半径が$d$である$p$次元超球の体積は係数を$k_p$のように表せば $$ V_p(d)=k_pd^ p $$ である.単位超球$B$内にデータが一様分布しているので,その確率密度関数は $$ p(X)= \left\{ \begin{array}{ll} 1/k_p & (\boldsymbol{x}\in B)\\ 0 & (\text{otherwise}) \end{array} \right. $$
である.
うち,距離$d=|\boldsymbol{x}|$に対して最も原点に近いデータ点$m=\min(\mathcal{D})$以上であるような確率,すなわち,$P(m<d)$は $$ \begin{eqnarray} P(m<d)&=&P(|\boldsymbol{x_i}|\geq d,\forall\boldsymbol{x_i}\in\mathcal{D})\\ &=&\prod_{\boldsymbol{x_i}\in\mathcal{D}}P(|\boldsymbol{x_i}|\geq d)\\ &=&\prod_{\boldsymbol{x_i}\in\mathcal{D}}(1-P(|\boldsymbol{x_i}|<d))\\ &=&\prod_{\boldsymbol{x_i}\in\mathcal{D}}\left(1-\int_{|\boldsymbol{x}|<d}p(\boldsymbol{x})d\boldsymbol{x}\right)\\ &=&\prod_{\boldsymbol{x_i}\in\mathcal{D}}\left(1-\frac{1}{k_p}\int_{|\boldsymbol{x}|<d}d\boldsymbol{x}\right)\\ &=&\prod_{\boldsymbol{x_i}\in\mathcal{D}}\left(1-d^ p\right)\\ &=&(1-d^ p)^ N \end{eqnarray} $$ これの中央値を考えると $$ \begin{eqnarray} (1-d^ p)^ N&=&\frac{1}{2}\\ d&=&\left(1-\left(\frac{1}{2}\right)^ {\frac{1}{N}}\right)^ {\frac{1}{p}} \end{eqnarray} $$ となる.$N=500,p=10$の場合,$d\approx0.52$となり,最近の点の中央値は境界までの距離の半分以上の位置にあることを示している.そのため,これは近傍点を用いた推論が極めて不安定なものになることを示唆しているといえる.
さらに,一般に標本化の密度は$N^ {1/p}$に比例するといわれている.$p=1$では$N=100$で十分な予測ができていたとしても,$p=10$ではこの条件と同様に密であるためには$N=100^ {10}$もの標本数が必要となる.
つぎに,実分布が$Y=f(X)=\exp(-8|X|^ 2)$という関係にあり,$\boldsymbol{x}$が$p$次元一様分布$U(-1,1)$から得られており,計測ノイズのないようなデータセットを考える.まず,このデータセットに対して$\boldsymbol{x}_0=0$に対する出力$y_0$を予測するといったタスクを考えると,$\boldsymbol{x_0}$に対する期待予測誤差は$f(0)$の平均二乗誤差(MSE)に相当する.ここで,平均二乗誤差は以下のように分解できる. $$ \begin{eqnarray} \text{MSE}(\boldsymbol{x_0})&=&\mathbb{E}_{\mathcal{T}}[(f(x_0)-\hat{y}_0)^ 2]\\ &=&\mathbb{E}_{\mathcal{T}}[(\hat{y}_0-\mathbb{E}_{\mathcal{T}}[\hat{y}_0]+\mathbb{E}_{\mathcal{T}}[\hat{y}_0]-f(x_0))^ 2]\\ &=&\mathbb{E}_{\mathcal{T}}[(\hat{y}_0-\mathbb{E}_{\mathcal{T}}[\hat{y_0}])^ 2+(\mathbb{E}_{\mathcal{T}}[\hat{y_0}]-f(x_0))^ 2+2(\hat{y}_0-\mathbb{E}_{\mathcal{T}}[\hat{y_0}])(\mathbb{E}_{\mathcal{T}}[\hat{y}_0]-f(x_0))]\\ &=&\mathbb{E}_{\mathcal{T}}[(\hat{y}_0-\mathbb{E}_{\mathcal{T}}[\hat{y}_0])^ 2]+ (\mathbb{E}_{\mathcal{T}}[\hat{y}_0]-f(x_0))^ 2+2\mathbb{E}_{\mathcal{T}}[(\hat{y}_0-\mathbb{E}_{\mathcal{T}}[\hat{y}_0])] (\mathbb{E}_{\mathcal{T}}[\hat{y}_0]-f(x_0))\\ &&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(\because \mathbb{E}_{\mathcal{T}}[\hat{y}],f(x_0)は定数)\\ &=&\text{Var}_{\mathcal{T}}[\hat{y}_0]+\text{Bias}_{\mathcal{T}}^ 2[\hat{y}_0] \end{eqnarray} $$ と,バイアス項とバリアンス(分散)項に分解することができる.このバイアスバリアンス分解は任意の問題設定において適用が可能である.
実装例
ps = np.arange(1, 11) b = [] v = [] for p in ps: x = np.random.random((1000, p)) * 2 - 1 x_test = np.zeros((1, p)) y = np.exp(-8*np.linalg.norm(x, axis=1, keepdims=True)**2) y_test = np.exp(-8*np.linalg.norm(x_test, axis=1, keepdims=True)**2) # 図2.8の場合はこちらです # y = .5*(x + 1) ** 3 # y_test = .5*(x_test + 1) ** 3 # if p != 1: # y[:, 1:] = 1 # y_test[:, 1:] = 1 model = KNN(k=1) model.fit(x, y) y_pred = model.predict(x_test) bias = ((y_test - y_pred)**2).mean() var = np.var(y_pred, axis=1).mean() b.append(bias.ravel()) v.append(var.ravel()) b = np.array(b) v = np.array(v) plt.figure(figsize=(7, 5)) plt.plot(ps, b, label="Bias") plt.plot(ps, v, label="Variance") plt.legend()
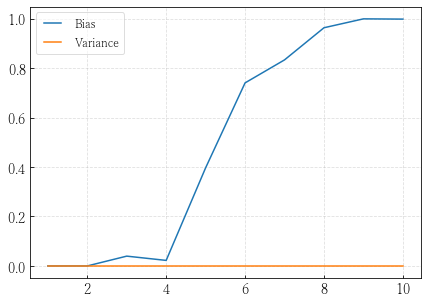
この場合は問題設定が大げさであるが,同様な問題は複雑なデータに関しても起こることが知られている.低次元でうまくいくようなモデルを,そのデータ数を変えずに高次元に対して応用した場合,思うような精度が出ず,必要となるデータ数が指数関数的に増加してしまう.
つぎに,線形モデルに$\epsilon\sim\mathcal{N}(0, \sigma^ 2)$の摂動が加わった $$ Y=X^ T\boldsymbol{\beta}+\epsilon $$ のモデルを最小二乗法で近似する場合を考える.
誤差項が加わったこの場合の期待予測誤差は
$$ \text{EPE}(\boldsymbol{x_0})=\sigma^ 2+\text{Var}_{\mathcal{T}}[\hat{y}_0]+\text{Bias}^ 2[\hat{y}_0] $$
となる.このモデルの下での最小二乗推定は不偏であることが知られており, $$ \text{Var}[\hat{y}_0]=\mathbb{E}_{\mathcal{T}}[\boldsymbol{x}_0^ T(X^ TX)^ {-1}\boldsymbol{x}_0\sigma^ 2] $$ である(証明は略.というより演習2.5が解けない) ので,共分散$\text{Cov}(X)$は$\mathbb{E}[X]\rightarrow0,N\rightarrow\infty$のもとでは $$ \text{Cov}(X)=\mathbb{E}[(X-\mu)(X-\mu)^ T]=\mathbb{E}[XX^ T]-\mu\mu^ T $$ と変形できることから,$\text{Cov}(X)\rightarrow\mathbb{E}[XX^ T]$であり,不偏であることから, $$ \mathbb{E}_{\boldsymbol{x}_0}[\text{EPE}(\boldsymbol{x}_0)]\sim\mathbb{E}_{\boldsymbol{x}_0}[\boldsymbol{x}_0^ T(X^ TX)^ {-1}\boldsymbol{x}_0\sigma^ 2]/N+\sigma^ 2 $$ $\boldsymbol{x}_0^ T(X^ TX)^ {-1}\boldsymbol{x}_0$はスカラーであり,スカラー値は自身の転置と当たり前ながら等しいので転置行列の性質$\text{tr}(AB)=\text{tr}(BA)$から, $$ \mathbb{E}_{\boldsymbol{x}_0}[\boldsymbol{x}_0^ T(X^ TX)^ {-1}\boldsymbol{x}_0]=\text{tr}(\mathbb{E}_{\boldsymbol{x}_0}[\boldsymbol{x}_0\boldsymbol{x}_0^ T] (X^ TX)^ {-1})=\text{tr}(\text{Cov}(X)\text{Cov}(X)^ {-1})=p $$ となり,結局 $$ \mathbb{E}_{\boldsymbol{x}_0}[\text{EPE}(\boldsymbol{x}_0)]=\sigma^ 2\left(\frac{p}{N}+1\right) $$ となる.
すなわち,最小二乗法では$N$を大きく,$\sigma^ 2$を小さくすることでバリアンスの次元数の増加に伴う線形増加を微小なものへと抑えることが可能であることを意味している.